Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Factoring Calculator
\text{Factor:}
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
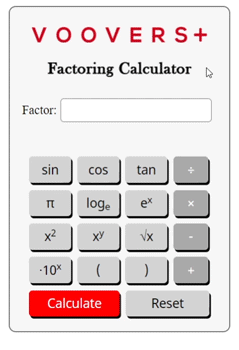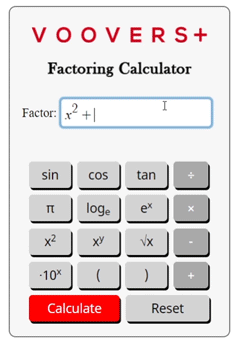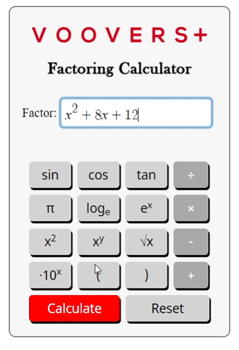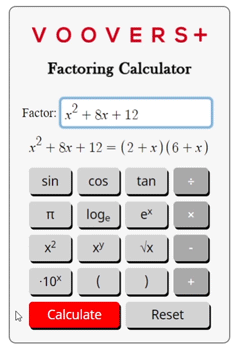
Lesson on Factoring
Lesson Contents
How to Factor a Perfect Square Trinomial
A perfect square trinomial is a polynomial of three terms that can be directly factored into a squared quantity. The formulas for factoring perfect square trinomials are given as:
x2 + 2ax + a2 = (x + a)2
x2 – 2ax + a2 = (x – a)2
Where x is the variable and a is a constant. When a polynomial is recognized to follow the perfect square trinomial pattern, it can directly be factored using the applicable formula.
How to Factor a Difference of Squares
A difference of squares binomial is a polynomial with two terms that can directly be factored into two quantities with opposite signs. The formula for factoring a difference of squares is given as:
x2 – a2 = (x + a)(x – a)
Where x is the variable and a is a constant. When we recognize that a polynomial follows this pattern, we may directly factor it using the difference of squares formula.
How to Factor any Polynomial
When a polynomial does not follow any pattern that gives us a shortcut for direct factorization, we may use a method called completing the square (see our lesson for full tutorial). Completing the square does not provide a pure factored form of an expression because it adds numbers to both sides of an equation.
However, completing the square does enable us to determine the zeroes or “roots” of an equation by converting it to a factored form. For example, we can set y = 0 in the equation y = x2 + 6x + 1, which gives us x2 + 6x + 1 = 0. Completing the square will provide a factored form and tell us the zeroes.
How the Calculator Works
This factoring calculator is coded in the language JavaScript (JS) and uses a computer algebra system (CAS) to perform factoring. The calculator runs inside the JS engine of your device’s internet browser which is how it gets instant solutions. It does not communicate with a server and does not need to refresh the webpage to show the answer.
Your inputted polynomial or expression is fed to the CAS where several steps are performed to factor it. All variables and numbers are treated as symbols, which preserves their exact value as inputted. Once the final answer is calculated, it is converted to LaTeX (a math rendering language) and displayed in the answer area of the calculator.
