What is a Tangent Plane?

A tangent plane is a plane that is tangent to a smooth surface (characterized by a differentiable function f ) at a specified point.

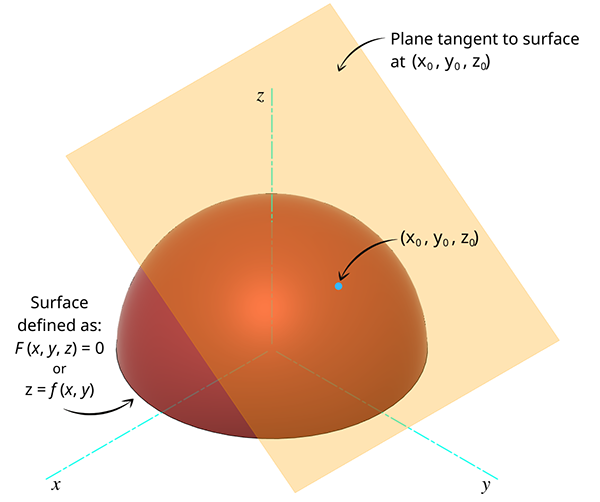
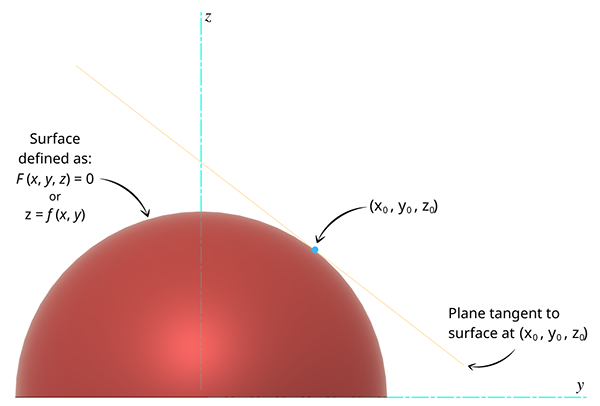
Why do we Learn about Tangent Planes?

Tangent planes are useful for approximating multivariable functions. This is similar to approximating single variable functions with the use of tangent lines. In the case of tangent planes, we can:

1. Find the plane that is tangent to a three dimensional surface at a specific point.
2. Use the resulting tangent plane equation to approximate function outputs that are reasonably close to our initial point.

How does this translate to reality? We can utilize tangent planes to approximate the lift force of an airfoil (cross-section of an airplane's wing in this case) with varying altitudes and speeds based on preliminary test data.

It is important to note that when we say that the tangent plane is tangent to a surface, the surface does not have to be a physical object. In this case, the three dimensional surface we will be discussing is composed of all the possible lift force values (data points) based on the air's density and the velocity of the airflow over the airfoil.

Think of the hemisphere from Figure 1 and Figure 2 as a bunch of numbers (z-values) that depend on the values of x and y.

Now, let's take a closer look at the lift equation to understand how we can linearly approximate lift values using tangent planes.

$$\begin{align} L = C_{L} \frac{\rho V^{2}}{2}A \end{align}$$

Where L is the lift force, C_L is the lift coefficient, ρ is the air density at a particular altitude, V is the velocity of the airflow over the wing, and A is the wing area.

If we hold C_L and A constant, then we have a function L = f (ρ, V). If we have initial data on what the lift force is for a given air density (ρ) and velocity (V), then we can find the equation of the plane tangent to the surface L = f (ρ, V) at (ρ₀, V₀). We can then use the tangent plane equation to approximate other lift values that are sufficiently close to our initial parameters (ρ₀, V₀).

How to Find the Equation of a Tangent Plane

To find the equation of a tangent plane, we need to begin by looking at how the surface in three dimensional space is defined. The equation of the aforementioned surface can be defined in two ways:

1. As a function F (x, y, z) = 0
2. Or, as a function z = f (x, y)

Tangent Plane Equation if Surface is Defined as F(x, y, z) = 0

If we define a surface with a function F(x, y, z) = 0, the general equation for the plane tangent to the surface at the specified point (x₀, y₀, z₀) is:

$$\begin{align} & F_{x}(x_{0}, y_{0}, z_{0})(x \; - \; x_{0}) + F_{y}(x_{0}, y_{0}, z_{0})(y \; - \; y_{0}) + F_{z}(x_{0}, y_{0}, z_{0})(z \; - \; z_{0}) = 0 \hspace{10ex} \bf{(1)} \end{align}$$

Where x₀ is the given x coordinate, y₀ is the given y coordinate, and z₀ is the given z coordinate. NOTE: If you are only given x₀ and y₀, you can rearrange your given function into the form: z = f (x, y) and plug in the values x₀ and y₀ to obtain z₀. In other words, z₀ = f (x₀, y₀).

Additionally:

$$\begin{align} F_{x}(x_{0}, y_{0}, z_{0}) = \frac{ \delta F}{\delta x} \text{ evaluated at } (x_{0}, y_{0}, z_{0}) \\ \\ F_{y}(x_{0}, y_{0}, z_{0}) = \frac{ \delta F}{\delta y} \text{ evaluated at } (x_{0}, y_{0}, z_{0}) \\ \\ F_{z}(x_{0}, y_{0}, z_{0}) = \frac{ \delta F}{\delta z} \text{ evaluated at } (x_{0}, y_{0}, z_{0}) \end{align}$$

The steps to populate the general equation of the tangent plane are as follows:

1. Take the partial derivative of F (x, y, z) = 0 with respect to x. This is referred to as F_x.
2. Take the partial derivative of F (x, y, z) = 0 with respect to y. This is referred to as F_y.
3. Take the partial derivative of F (x, y, z) = 0 with respect to z. This is referred to as F_z.
4. Plug the values for x₀, y₀, and z₀ into the result for F_x to obtain the value for F_x (x₀, y₀, z₀).
5. Plug the values for x₀, y₀, and z₀ into the result for F_y to obtain the value for F_y (x₀, y₀, z₀).
6. Plug the values for x₀, y₀, and z₀ into the result for F_z to obtain the value for F_z (x₀, y₀, z₀).
7. Plug the values obtained from steps 4 - 6 into the general equation of the tangent plane (Equation 1). Additionally, plug in the values for x₀, y₀, and z₀.
8. Simplify the equation.

Tangent Plane Equation if Surface is Defined as z = f(x, y)

If we define a surface with a function z = f (x, y), the general equation for the plane tangent to the surface at the specified point (x₀, y₀, f (x₀, y₀)) is:

$$\begin{align} & z = f_{x}(x_{0}, y_{0})(x \; - \; x_{0}) + f_{y}(x_{0}, y_{0})(y \; - \; y_{0}) + f(x_{0}, y_{0}) \hspace{10ex} \bf{(2)} \end{align}$$

Where x₀ is the given x coordinate, y₀ is the given y coordinate, and f (x₀, y₀) is the given function evaluated at x₀ and y₀.

Additionally:

$$\begin{align} f_{x}(x_{0}, y_{0}) = \frac{ \delta f}{\delta x} \text{ evaluated at } (x_{0}, y_{0}) \\ \\ f_{y}(x_{0}, y_{0}) = \frac{ \delta f}{\delta y} \text{ evaluated at } (x_{0}, y_{0})\end{align}$$

The steps to populate the general equation of the tangent plane are as follows:

1. Plug the values for x₀ and y₀ into the given function z = f (x, y) to obtain the value for f (x₀, y₀).
2. Take the partial derivative of z = f (x, y) with respect to x. This is referred to as f_x.
3. Take the partial derivative of z = f (x, y) with respect to y. This is referred to as f_y.
4. Plug the values for x₀ and y₀ into the result for f_x to obtain the value for f_x (x₀, y₀).
5. Plug the values for x₀ and y₀ into the result for f_y to obtain the value for f_y (x₀, y₀).
6. Plug the values obtained from steps 4 and 5 into the general equation of the tangent plane (Equation 2). Additionally, plug in the values for x₀ and y₀.
7. Simplify the equation.

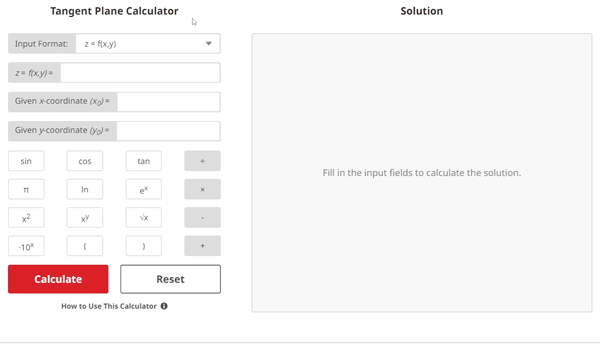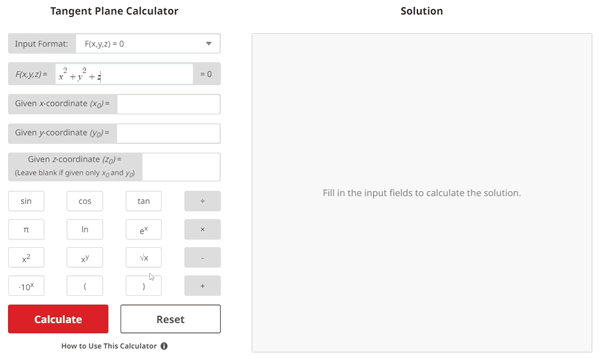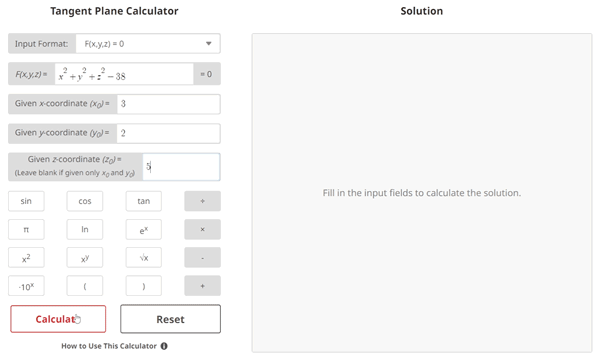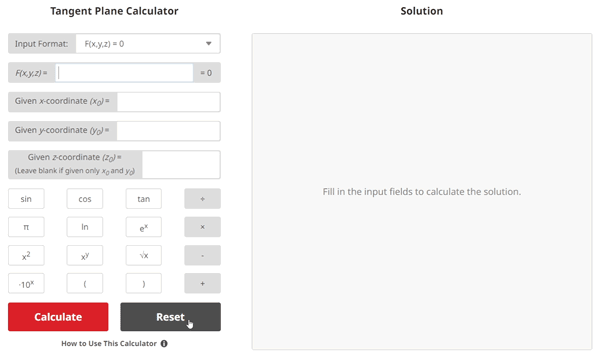
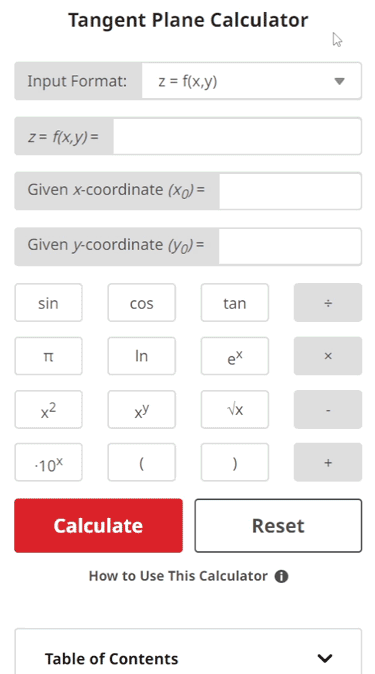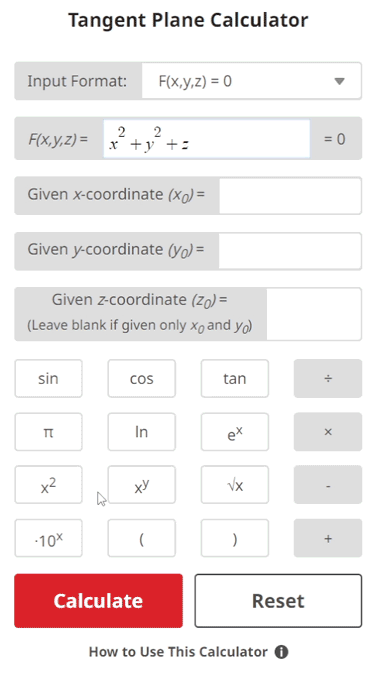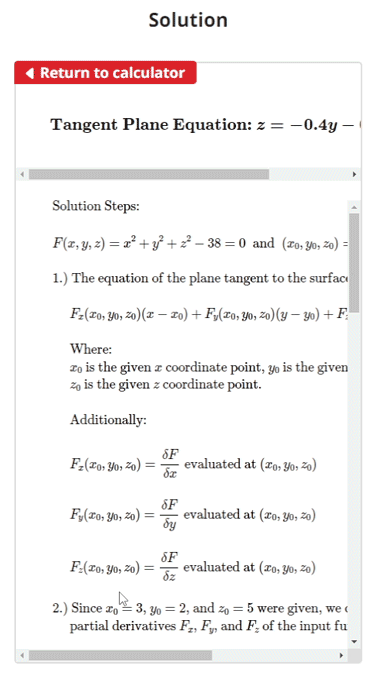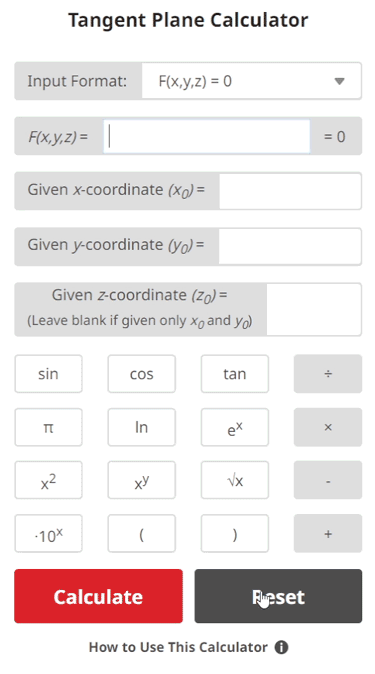
Example Problem 1: F(x, y, z) = 0 with (x0, y0, z0) Given

$$\begin{align}& \text{Solution Steps:} \hspace{57ex}& \\ \\ & F(x,y,z) = x^2+y^2+z^2-38 = 0 \; \text{ and } \;(x_{0}, y_{0}, z_{0}) = (3, 2, 5)\\ \\ & \text{1.) The equation of the plane tangent to the surface } F(x, y, z) = 0 \text{ is given as:} \\ \\ & \hspace{3ex} F_{x}(x_{0}, y_{0}, z_{0})(x - x_{0}) + F_{y}(x_{0}, y_{0}, z_{0})(y - y_{0}) + F_{z}(x_{0}, y_{0}, z_{0})(z - z_{0}) = 0 \\ \\ & \hspace{3ex} \text{Where: } \\ & \hspace{3ex} x_{0} \text{ is the given } x \text{ coordinate point, } y_{0} \text{ is the given } y \text{ coordinate point, and }\\ & \hspace{3ex}z_{0} \text{ is the given } z \text{ coordinate point.}\\ \\ & \hspace{3ex} \text{Additionally:} \\ \\ & \hspace{3ex} F_{x}(x_{0}, y_{0}, z_{0}) = \frac{\delta F}{\delta x} \text{ evaluated at }(x_{0}, y_{0}, z_{0}) \\ \\ & \hspace{3ex} F_{y}(x_{0}, y_{0}, z_{0}) = \frac{\delta F}{\delta y} \text{ evaluated at }(x_{0}, y_{0}, z_{0}) \\ \\ & \hspace{3ex} F_{z}(x_{0}, y_{0}, z_{0}) = \frac{\delta F}{\delta z} \text{ evaluated at }(x_{0}, y_{0}, z_{0})\\ \\ &\text{2.) Since } x_{0} = 3\text{, } y_{0} = 2\text{, and } z_{0} = 5\text{ were given, we can begin finding the} \\ & \hspace{3ex} \text{partial derivatives } F_{x} \text{, } F_{y} \text{, and } F_{z} \text{ of the input function } F(x, y, z) \text{.}\\ \\ &\text{3.) Finding } F_{x} \text{, } F_{y} \text{, and } F_{z} \text{ of input function } F(x, y, z) = x^2+y^2+z^2-38 = 0:\\ \\ & \text{3.1) } F_{x} = \frac{\delta F(x, y, z)}{\delta x} \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta x} = 2 x\\ \\ & \text{3.2) } F_{y} = \frac{\delta F(x, y, z)}{\delta y} \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta y} = 2 y\\ \\ & \text{3.3) } F_{z} = \frac{\delta F(x, y, z)}{\delta z} \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta z} = 2 z\\ \\ &\text{4.) Plug the values for } x_{0} \text{, } y_{0} \text{, and } z_{0} \text{ into each result for } F_{x} \text{, } F_{y} \text{, and } F_{z} \\ & \hspace{3ex} \text{found in steps 3.1 - 3.3:}\\ \\ & \text{4.1) } F_{x}(x_{0}, y_{0}, z_{0}) = \frac{\delta F(x, y, z)}{\delta x} \text{ evaluated at } (x_{0} = 3, y_{0} = 2, z_{0} = 5) \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta x} = 2 x\\ \\ & \hspace{5ex} \Longrightarrow \left. \frac{\delta F(x, y, z)}{\delta x} \right|_{(3, \;2, \; 5)} = 2(3) = 6\\ \\ & \hspace{5ex} \Longrightarrow \text{Therefore, } F_{x}(x_{0}, y_{0}, z_{0}) = 6\\ \\ & \text{4.2) } F_{y}(x_{0}, y_{0}, z_{0}) = \frac{\delta F(x, y, z)}{\delta y} \text{ evaluated at } (x_{0} = 3, y_{0} = 2, z_{0} = 5) \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta y} = 2 y\\ \\ & \hspace{5ex} \Longrightarrow \left. \frac{\delta F(x, y, z)}{\delta y} \right|_{(3, \;2, \; 5)} = 2(2) = 4\\ \\ & \hspace{5ex} \Longrightarrow \text{Therefore, } F_{y}(x_{0}, y_{0}, z_{0}) = 4\\ \\ & \text{4.3) } F_{z}(x_{0}, y_{0}, z_{0}) = \frac{\delta F(x, y, z)}{\delta z} \text{ evaluated at } (x_{0} = 3, y_{0} = 2, z_{0} = 5) \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta F(x, y, z)}{\delta z} = 2 z\\ \\ & \hspace{5ex} \Longrightarrow \left. \frac{\delta F(x, y, z)}{\delta z} \right|_{(3, \;2, \; 5)} = 2(5) = 10\\ \\ & \hspace{5ex} \Longrightarrow \text{Therefore, } F_{z}(x_{0}, y_{0}, z_{0}) = 10\\ \\ &\text{5.) Plug the following values into the equation of the tangent plane} \\ & \hspace{3ex} \text{for } F(x, y, z) = 0 \text{ and solve for } z \text{:} \\ \\ & \hspace{3ex} \boxed{x_{0} = 3\hspace{3ex} y_{0} = 2\hspace{3ex} z_{0} = 5} \\ \\ & \hspace{3ex} \boxed{F_{x}(x_{0}, y_{0}, z_{0}) = 6\hspace{3ex} F_{y}(x_{0}, y_{0}, z_{0}) = 4\hspace{3ex} F_{z}(x_{0}, y_{0}, z_{0}) = 10}\\ \\ & \text{5.1) The equation of the plane tangent to the surface } F(x, y, z) = 0 \\ & \hspace{5ex} \text{ is given as:} \\ \\ & \hspace{5ex} F_{x}(x_{0}, y_{0}, z_{0})(x - x_{0}) + F_{y}(x_{0}, y_{0}, z_{0})(y - y_{0}) + F_{z}(x_{0}, y_{0}, z_{0})(z - z_{0}) = 0 \\ \\ & \hspace{5ex} \Longrightarrow (6)(x - (3)) + (4)(y - (2)) + (10)(z - (5)) = 0 \\ \\ & \hspace{5ex} \Longrightarrow- 76 + 10 z + 4 y + 6 x = 0\\ \\ & \text{5.2) Solving for } z \text{, we get:} \\ \\ & \hspace{5ex} \Longrightarrow z = - 0.4 y - 0.6 x + 7.6\\ \\ & \text{Therefore, the equation of the plane tangent to the surface } \\ & F(x,y,z) = x^2+y^2+z^2-38 = 0 \; \text{ at } \;(x_{0}, y_{0}, z_{0}) = (3, 2, 5)\text{ is: } \\ \\ & \boxed{\boxed{z = - 0.4 y - 0.6 x + 7.6}}\\ & \end{align}$$

Example Problem 2: z = f(x, y) with (x0, y0) Given

$$\begin{align}& \text{Solution Steps:} \hspace{57ex}& \\ \\ & z = f(x,y) = x^2+2y^2-1\; \text{ and } \; (1, 2)\\ \\ & \text{1.) The equation of the plane tangent to the surface } z = f(x, y) \text{ at the point } \\ & \hspace{3ex} (x_{0}, y_{0}, f(x_{0}, y_{0})) \text{ is given as:} \\ \\ & \hspace{3ex} z = f_{x}(x_{0}, y_{0})(x - x_{0}) + f_{y}(x_{0}, y_{0})(y - y_{0}) + f(x_{0}, y_{0}) \\ \\ & \hspace{3ex} \text{Where: } \\ & \hspace{3ex} x_{0} \text{ is the given } x \text{ coordinate point, } y_{0} \text{ is the given } y \text{ coordinate point, and }\\ & \hspace{3ex} f(x_{0}, y_{0}) \text{ is the input function evaluated at } (x_{0}, y_{0}) \\ \\ & \hspace{3ex} \text{Additionally:} \\ \\ & \hspace{3ex} f_{x}(x_{0}, y_{0}) = \frac{\delta f}{\delta x} \text{ evaluated at }(x_{0}, y_{0}) \\ \\ & \hspace{3ex} f_{y}(x_{0}, y_{0}) = \frac{\delta f}{\delta y} \text{ evaluated at }(x_{0}, y_{0})\\ \\ &\text{2.) Begin by evaluating } f(x_{0}, y_{0}):\\ \\ & \text{2.1) } f(x,y) = x^2+2y^2-1\text{, } x_{0} = 1\text{, and } y_{0} = 2\\ \\ & \hspace{5ex} \Longrightarrow f(1, 2) = -1+2(2)^2+(1)^2\\ \\ & \hspace{5ex} \Longrightarrow f(x_{0}, y_{0}) = f(1, 2) = 8\\ \\ &\text{3.) Now that we have } x_{0} \text{, } y_{0} \text{, and } f(x_{0}, y_{0}) \text{, we can begin finding } f_{x} \text{ and } f_{y} \\ & \hspace{3ex} \text{of input function } \; z = f(x, y) = x^2+2y^2-1:\\ \\ & \text{3.1) } f_{x} = \frac{\delta f(x, y)}{\delta x} \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta f(x, y)}{\delta x} = 2 x\\ \\ & \text{3.2) } f_{y} = \frac{\delta f(x, y)}{\delta y} \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta f(x, y)}{\delta y} = 4 y\\ \\ &\text{4.) Plug the values for } x_{0} \text{ and } y_{0} \text{ into each result for } f_{x} \text{ and } f_{y} \\ & \hspace{3ex} \text{found in steps 3.1 and 3.2:}\\ \\ & \text{4.1) } f_{x}(x_{0}, y_{0}) = \frac{\delta f(x, y)}{\delta x} \text{ evaluated at } (x_{0} = 1, y_{0} = 2) \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta f(x, y)}{\delta x} = 2 x\\ \\ & \hspace{5ex} \Longrightarrow \left. \frac{\delta f(x, y)}{\delta x} \right|_{(1, \;2)} = 2(1) = 2\\ \\ & \hspace{5ex} \Longrightarrow \text{Therefore, } f_{x}(x_{0}, y_{0}) = 2\\ \\ & \text{4.2) } f_{y}(x_{0}, y_{0}) = \frac{\delta f(x, y)}{\delta y} \text{ evaluated at } (x_{0} = 1, y_{0} = 2) \\ \\ & \hspace{5ex} \Longrightarrow \frac{\delta f(x, y)}{\delta y} = 4 y\\ \\ & \hspace{5ex} \Longrightarrow \left. \frac{\delta f(x, y)}{\delta y} \right|_{(1, \;2)} = 4(2) = 8\\ \\ & \hspace{5ex} \Longrightarrow \text{Therefore, } f_{y}(x_{0}, y_{0}) = 8\\ \\ &\text{5.) Plug the following values into the equation of the tangent plane} \\ & \hspace{3ex} \text{for } z = f(x, y) \text{ and solve for } z \text{:} \\ \\ & \hspace{3ex} \boxed{x_{0} = 1\hspace{3ex} y_{0} = 2\hspace{3ex} f(x_{0}, y_{0}) = 8} \\ \\ & \hspace{3ex} \boxed{f_{x}(x_{0}, y_{0}) = 2\hspace{3ex} f_{y}(x_{0}, y_{0}) = 8}\\ \\ & \text{5.1) The equation of the plane tangent to the surface } z = f(x, y) \text{ at } \\ & \hspace{5ex} \text{the point } (x_{0}, y_{0}, f(x_{0}, y_{0})) \text{ is given as:} \\ \\ & \hspace{5ex} z = f_{x}(x_{0}, y_{0})(x - x_{0}) + f_{y}(x_{0}, y_{0})(y - y_{0}) + f(x_{0}, y_{0}) \\ \\ & \hspace{5ex} \Longrightarrow z = (2)(x - (1)) + (8)(y - (2)) + (8)\\ \\ & \text{5.2) After simplifying, we get:} \\ \\ & \hspace{5ex} \Longrightarrow z = - 10 + 2 x + 8 y\\ \\ & \text{Therefore, the equation of the plane tangent to the surface } \\ & z = f(x,y) = x^2+2y^2-1 \; \text{ at } \; (1, 2) \text{ is: } \\ \\ & \boxed{\boxed{z = - 10 + 2 x + 8 y}}\\ & \end{align}$$

How the Calculator Works

The Tangent Plane Calculator uses a combination of HTML (Hypertext Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). These languages allow the user to type in their desired inputs into a virtual interface, interact with the calculator, and see the custom step-by-step solution to their problem.

When an individual enters their desired inputs and clicks "Calculate", the entered values are stored as JavaScript variables which are used for calculations and defining other variables that lead to the final answer.

The answer and solution steps are then showed to the user in an easy-to-follow format that is visually rendered by LaTeX (a document preparation system).

The output fields and calculator are styled with CSS. This includes the size of the calculator, color of the buttons, and all the other visual properties of these elements.