Relative Extrema Calculator
Solution


Relative Extrema Lesson
What are Relative Extrema?
The relative extrema of a function are all of the locations of relative maximums and relative minimums.
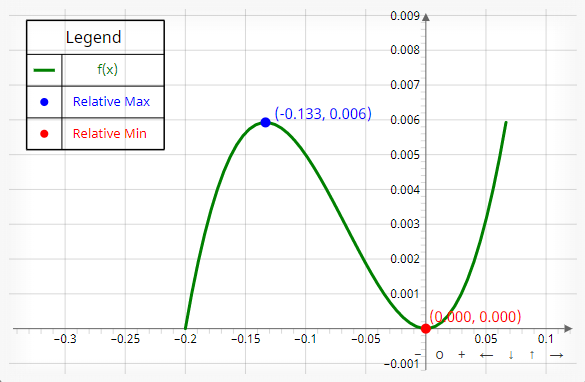
The word "extrema" is plural for the word "extremum". An extremum is a point where a function has its largest or smallest value.
If an extremum point is the most extreme value of the function on the entire domain, it is called an absolute extremum. The largest value for a function on the entire domain is called an absolute maximum and the smallest value is called an absolute minimum.
If an extremum point occurs where the function's value changes from increasing to decreasing (a peak) or where the function changes from decreasing to increasing (a trough), it is called a relative extremum because it is an extreme point relative to the function's values surrounding it.
Locations where the function's value changes from increasing to decreasing (a peak) are called relative maximums. Locations where the function's value changes from decreasing to increasing (a trough) are called relative minimums.
In some cases, a relative extremum point can also be an absolute extremum point. For example, f(x) = x2 changes from decreasing to increasing at x = 0 which is a relative minimum. However, the smallest value of the function on its entire domain also occurs at x = 0 so the relative minimum is also the absolute minimum.
Why do we Learn About Relative Extrema?
Since this topic has countless real-world applications, let's choose just one to dive into here: finding relative extrema can help us in creating sustainable, clean energy for the future with nuclear fusion power.
Nuclear fusion is when two atoms fuse together and release enormous amounts of energy, usually in the form of heat. In nuclear fusion power, this heat is utilized to boil water, creating pressurized steam which turns a steam turbine attached to an electric generator.
Nuclear fusion is powerful and the fuel can be abundantly found in the Earth's oceans, but there's a big catch: a nuclear fusion reaction is extremely difficult to start and sustain.
One of the approaches to starting and sustaining nuclear fusion is with a system called inertial confinement fusion, which uses lasers to impart extreme heat and pressure onto a piece of fuel, causing a fusion reaction to occur.

Credit: Damien Jemison/LLNL
There is an incredible demand placed on these lasers, but fortunately, we can use the concept of relative extrema to ensure the lasers will have enough power for the fusion reaction. Because lasers only perform optimally under very particular operating parameters, we can make this into an optimization problem.
The image below is an example graph of a laser's wavelength versus intensity function. Since we want to maximize a laser's output intensity, the relative maximums on this graph will correspond to the wavelength range(s) that the laser should be run at.
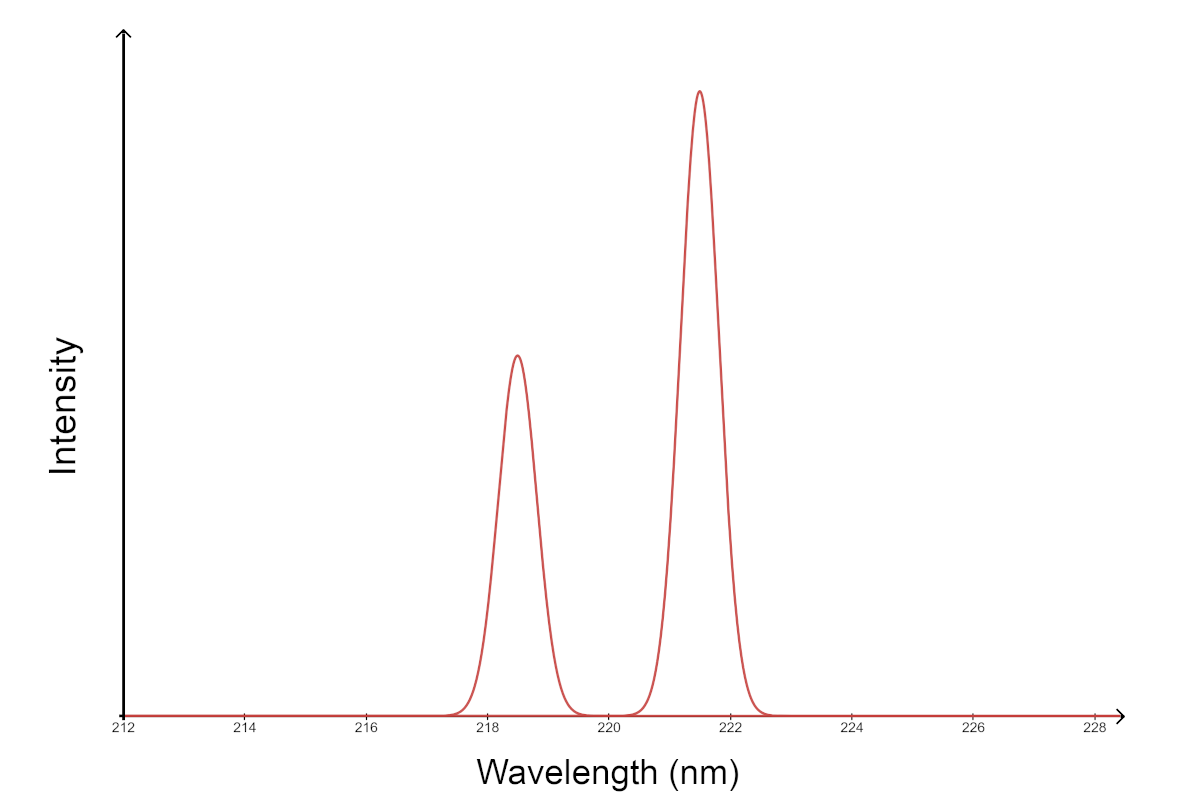
By finding the relative extrema of a laser's wavelength versus intensity function, we learn critical information about the ideal operating parameters of the laser. We may then use this information to plan, design, and optimize a laser system for use in a cutting-edge application such as nuclear fusion power!
How to Find the Relative Extrema of a Function
The first major step to finding the relative extrema of a function f(x) is to find all critical points of the function f(x) on the domain -∞ < x < ∞.
Critical points x = c are located where f(c) exists and either f ‘(c) = 0 or f ‘(c) is undefined.
The steps for finding the critical points are as follows:
- Take the derivative of f(x) to get f ‘(x)
- Find all x values where f ‘(x) = 0 or where f ‘(x) is undefined
- Plug the x values obtained from step 2 into f(x) to test whether or not the function exists at each respective x value
The x values found in step 2 where f(x) does exist can be taken as critical points x = c since f(x) exists at these points and they lie within the given domain.
The second major step to finding the relative extrema is to create and test intervals between the critical points to determine where f(x) is increasing or decreasing.
We will create intervals bounded by the function's critical points. And since the domain is -∞ < x < ∞, we will also create a first interval that starts at x = -∞ and a last interval that ends at x = ∞.
To test each interval, we evaluate the derivative f '(x) at any point between the bounds of the respective interval. If the evaluation of f '(x) is positive, the function is increasing on that respective interval. If the evaluation of f '(x) is negative, the function is decreasing on that respective interval.
For example, if a function's critical points are x = -2 and x = 4, the test intervals and derivative test points will be as follows:
Test interval 1 is x = [-∞, -2] and derivative test point 1 can be x = -3.
Test interval 2 is x = [-2, 4] and derivative test point 2 can be x = 1.
Test interval 3 is x = [4, ∞] and derivative test point 3 can be x = 5.
The third and final major step to finding the relative extrema is to look across the test intervals for either a change from increasing to decreasing or from decreasing to increasing.
If either of these conditions is met, there is a relative extremum at the critical point between the respective intervals. Since we already checked if f(x) exists at each critical point, this third step will generate our final list of relative extrema x values.
Example Problem 1
$$\begin{align}& \hspace{2ex} \text{Find all relative extrema of } f(x) = \frac{2}{3}x^3-2x\\ \\ & \hspace{2ex} \text{To do this, we will:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Find the critical points of } f(x) \text{ on the domain } \: -\infty < x < \infty \\ \\ & \hspace{3ex} \text{2) Create and test intervals between critical points} \\ & \hspace{5ex} \text{to see where } f(x) \text{ is increasing or decreasing} \\ \\ & \hspace{3ex} \text{3) Determine where } f(x) \text{ changes from increasing to decreasing or} \\ & \hspace{5ex} \text{from decreasing to increasing to get relative extrema locations}\\ \\ & \text{1.1) Critical Points } \: x = c \: \text{ are found where: } f(c) \text{ exists} \\ & \hspace{4ex} \text{and one of the following two conditions is met:} \\ \\ & \hspace{5ex} \bullet f'(c) = 0 \\ \\ & \hspace{5ex} \text{*OR*} \\ \\ & \hspace{5ex} \bullet f'(c) \text{ is undefined}\\ \\ & \text{1.2) } f(x) = \frac{2}{3}x^3-2x\text{, find } f'(x) \text{:} \\ \\ & \hspace{4ex} f'(x) =2 {x}^{2} - 2\\ \\ & \text{1.3) Find } x \text{ values such that } f'(x) = 0 \text{ or } f'(x) \text{ is undefined } \\ & \hspace{4ex} \text{to get provisional critical points } c \text{ :} \\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} 2 {x}^{2} - 2 = 0 \\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} \text{After solving for } x \text{ we get } x =1,-1\\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} c =1,-1\\ \\ & \text{1.4) Since our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{(all real numbers), and our } c \text{ values} \\ & \hspace{4ex} \text{are real numbers, we will plug all of these } c \text{ values into } f(x) \text{ to get } f(c) \text{.}\\ \\ & \text{1.5) Plugging our real } c \text{ values into } f(x) \text{ to get } f(c) \text{, we get:}\\ \\ & \hspace{4ex} f(c_{1}) = \frac{2}{3}(1)^3-2(1) = -1.3333333333333333\\ \\ & \hspace{4ex} \text{Since } f(x) \text { exists at } c_{1}, \text{ there is a critical point at } c_{1} \text{ = } 1\\\\ \\ & \hspace{4ex} f(c_{2}) = \frac{2}{3}(-1)^3-2(-1) = 1.3333333333333333\\ \\ & \hspace{4ex} \text{Since } f(x) \text { exists at } c_{2}, \text{ there is a critical point at } c_{2} \text{ = } -1\\\\ \\ & \hspace{4ex} \text{Our critical points sorted from least to greatest:} \\ \\ & \hspace{4ex} x = -1,1\\ \\ & \text{2.1) To test for intervals of increase or decrease, we will evaluate the} \\ & \hspace{4ex} \text{derivative } f'(x) \text{ at a test x value } anywhere \; between \text{ each critical point.} \\ \\ & \hspace{4ex} \text{We will create intervals bounded by the critical points, and} \\ & \hspace{4ex} \text{because our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{we will also create:} \\ & \hspace{5ex} \bullet \text{A first interval that starts at } x = -\infty \\ & \hspace{5ex} \bullet \text{A last interval that ends at } x = \infty\\ \\ & \text{2.2) Interval }1\text{ is: } x = [-\infty, -1] \\ & \hspace{5ex} \text{Test x-value } = -2\\ & \hspace{5ex} f'(x) \text{ evaluated at the test x-value: } f'(-2) = 2 {(-2)}^{2} - 2 = 6\\ & \hspace{5ex} f'(x) >0, \text{ so } f(x) \text{ is} \; increasing\; on \; interval \;1.\\ \\ & \text{2.3) Interval }2\text{ is: } x = [-1, 1] \\ & \hspace{5ex} \text{Test x-value } = 0\\ & \hspace{5ex} f'(x) \text{ evaluated at the test x-value: } f'(0) = 2 {(0)}^{2} - 2 = -2\\ & \hspace{5ex} f'(x) <0, \text{ so } f(x) \text{ is} \; decreasing\; on \; interval \;2.\\ \\ & \text{2.4) Interval }3\text{ is: } x = [1, \infty] \\ & \hspace{5ex} \text{Test x-value } = 2\\ & \hspace{5ex} f'(x) \text{ evaluated at the test x-value: } f'(2) = 2 {(2)}^{2} - 2 = 6\\ & \hspace{5ex} f'(x) >0, \text{ so } f(x) \text{ is} \; increasing\; on \; interval \;3.\\ \\ & \text{3.1) To find the relative extrema, we will look across the} \\ & \hspace{4ex} \text{intervals for either of the following two conditions:} \\ \\ & \hspace{4ex} \bullet \text{ If } f(x) \text{ changes from increasing over one interval to decreasing} \\ & \hspace{7ex} \text{over the next interval (relative maximum)} \\ \\ & \hspace{4ex} \text{*OR*} \\ \\ & \hspace{4ex} \bullet \text{ If } f(x) \text{ changes from decreasing over one interval to increasing} \\ & \hspace{7ex} \text{over the next interval (relative minimum)} \\ \\ & \hspace{4ex} \text{If either condition is met, there is a relative extremum} \\ & \hspace{4ex} \text{at the critical point between the respective intervals.}\\ \\ & \text{3.2) Since } f(x) \text{ is }increasing\text{ on interval }1\text{ and is }decreasing\text{ on interval }2\text{,} \\ & \hspace{4ex} the \; first \; condition \; is \; met \text{ and there is } a \; relative \; maximum \text{ at the} \\ & \hspace{4ex} \text{respective critical point } x = -1\text{.}\\ \\ & \text{3.3) Since } f(x) \text{ is }decreasing\text{ on interval }2\text{ and is }increasing\text{ on interval }3\text{,} \\ & \hspace{4ex} the \; second \; condition \; is \; met \text{ and there is } a \; relative \; minimum \text{ at the} \\ & \hspace{4ex} \text{respective critical point } x = 1\text{.}\end{align}$$
Example Problem 2
$$\begin{align}& \hspace{2ex} \text{Find all relative extrema of } f(x) = \sqrt[3]{x}-12\\ \\ & \hspace{2ex} \text{To do this, we will:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Find the critical points of } f(x) \text{ on the domain } \: -\infty < x < \infty \\ \\ & \hspace{3ex} \text{2) Create and test intervals between critical points} \\ & \hspace{5ex} \text{to see where } f(x) \text{ is increasing or decreasing} \\ \\ & \hspace{3ex} \text{3) Determine where } f(x) \text{ changes from increasing to decreasing or} \\ & \hspace{5ex} \text{from decreasing to increasing to get relative extrema locations}\\ \\ & \text{1.1) Critical Points } \: x = c \: \text{ are found where: } f(c) \text{ exists} \\ & \hspace{4ex} \text{and one of the following two conditions is met:} \\ \\ & \hspace{5ex} \bullet f'(c) = 0 \\ \\ & \hspace{5ex} \text{*OR*} \\ \\ & \hspace{5ex} \bullet f'(c) \text{ is undefined}\\ \\ & \text{1.2) } f(x) = \sqrt[3]{x}-12\text{, find } f'(x) \text{:} \\ \\ & \hspace{4ex} f'(x) =\frac{1}{3 {x}^{\left(\frac{2}{3}\right)}}\\ \\ & \text{1.3) Find } x \text{ values such that } f'(x) = 0 \text{ or } f'(x) \text{ is undefined } \\ & \hspace{4ex} \text{to get provisional critical points } c \text{ :} \\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} \frac{1}{3 {x}^{\left(\frac{2}{3}\right)}} = 0 \\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} \text{After solving for } x \text{ we get } x =0\\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} c =0\\ \\ & \text{1.4) Since our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{(all real numbers), and our } c \text{ values} \\ & \hspace{4ex} \text{are real numbers, we will plug all of these } c \text{ values into } f(x) \text{ to get } f(c) \text{.}\\ \\ & \text{1.5) Plugging our real } c \text{ values into } f(x) \text{ to get } f(c) \text{, we get:}\\ \\ & \hspace{4ex} f(c_{1}) = \sqrt[3]{(0)}-12 = -12\\ \\ & \hspace{4ex} \text{Since } f(x) \text { exists at } c_{1}, \text{ there is a critical point at } c_{1} \text{ = } 0\\\\ \\ & \text{2.1) To test for intervals of increase or decrease, we will evaluate the} \\ & \hspace{4ex} \text{derivative } f'(x) \text{ at a test x value } anywhere \; between \text{ each critical point.} \\ \\ & \hspace{4ex} \text{We will create intervals bounded by the critical points, and} \\ & \hspace{4ex} \text{because our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{we will also create:} \\ & \hspace{5ex} \bullet \text{A first interval that starts at } x = -\infty \\ & \hspace{5ex} \bullet \text{A last interval that ends at } x = \infty\\ \\ & \text{2.2) Interval }1\text{ is: } x = [-\infty, 0] \\ & \hspace{5ex} \text{Test x-value } = -1\\ & \hspace{5ex} f'(x) \text{ evaluated at the test x-value: } f'(-1) = \frac{1}{3 {(-1)}^{\left(\frac{2}{3}\right)}} = 0.3333333333333333\\ & \hspace{5ex} f'(x) >0, \text{ so } f(x) \text{ is} \; increasing\; on \; interval \;1.\\ \\ & \text{2.3) Interval }2\text{ is: } x = [0, \infty] \\ & \hspace{5ex} \text{Test x-value } = 1\\ & \hspace{5ex} f'(x) \text{ evaluated at the test x-value: } f'(1) = \frac{1}{3 {(1)}^{\left(\frac{2}{3}\right)}} = 0.3333333333333333\\ & \hspace{5ex} f'(x) >0, \text{ so } f(x) \text{ is} \; increasing\; on \; interval \;2.\\ \\ & \text{3.1) To find the relative extrema, we will look across the} \\ & \hspace{4ex} \text{intervals for either of the following two conditions:} \\ \\ & \hspace{4ex} \bullet \text{ If } f(x) \text{ changes from increasing over one interval to decreasing} \\ & \hspace{7ex} \text{over the next interval (relative maximum)} \\ \\ & \hspace{4ex} \text{*OR*} \\ \\ & \hspace{4ex} \bullet \text{ If } f(x) \text{ changes from decreasing over one interval to increasing} \\ & \hspace{7ex} \text{over the next interval (relative minimum)} \\ \\ & \hspace{4ex} \text{If either condition is met, there is a relative extremum} \\ & \hspace{4ex} \text{at the critical point between the respective intervals.}\\ \\ & \text{3.2) Since } f(x) \text{ is }increasing\text{ on interval }1\text{ and is }increasing\text{ on interval }2\text{,} \\ & \hspace{4ex} neither \text{ of the conditions are met and there } is \; no \; relative \; extremum \\ & \hspace{4ex} \text{at the respective critical point } x = 0\text{.}\end{align}$$
How the Calculator Works
The Voovers Relative Extrema Calculator is built using HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). HTML creates the calculator's skeleton, CSS provides its styling, and JS gives it functionality.
When the calculate button is clicked, a JS function is activated which reads the user input, formats the function for JS use, and begins the process of finding all relative extrema.
From beginning to end, this process matches very closely with the process outlined in the lesson above. The main difference between solving by hand and what this calculator does is that computer hardware performs algebraic and calculus operations instead of a person.
Along the way, snapshots of the process are taken and later formatted for use as the solution steps. These solution steps are converted to a math rendering language called LaTeX, which allows the printing of visually appealing mathematical expressions. After calculations finish, the final answer and steps are fed to the solution area.




