How to Complete the Square

Completing the square is a method that gives us the ability to solve any quadratic equation. We complete the square by adding or subtracting a number from a quadratic to make it possible to factor.

We cannot solve the equation x² + 4x = 6 by immediately factoring, but we can solve it by completing the square.

By adding 4 to both sides of the equation we get x² + 4x + 4 = 10. We just completed the square, because now the left side is a perfect square and can be factored resulting in (x + 2)² = 10.

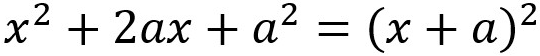
The Formula for Completing the Square

Now that we have seen what it looks like to complete the square, let's go over the formula that is used to complete the square. Remember that we added a number to both sides of the equation. Here's the formula that we use to determine what that number is:

x² + 2ax + a²

This is the format of a quadratic considered to be a "perfect square". Notice how the middle term's coefficient is 2a, while the term on the right is the constant a². This is because of how a perfect square quadratic is factored.

Using the Formula

For example, x² + 4x + 4 = (x + 2)².

(x + 2)² = (x + 2)(x + 2) = (x + a)(x + a)

In this case, a = 2. We can see how the constant inside of the parenthesis gets multiplied by itself when squaring the parenthesis by using the distributive property. This is where the a² comes from. The 2a comes from the x getting multiplied by the a twice and then combining both ax terms to make 2ax.

In summary, we need to make one side of our equation look like the perfect square formula so that we can factor. Once it's in factored form, solving for the zeroes/roots only requires taking the square root of both sides of the equation.

Completing the Square Example Problem

Find the zeroes of the equation x² + 6x + 1 = 0.

Solution:

1. By using the perfect square formula, we know that the coefficient in front of x is 2a. Since that term is 6x, 2ax = 6x. Therefore, a = 3.
2. Now let's figure out what the a² term will be. a² = 3² = 9.
3. The rightmost term in the quadratic is currently 1. We need it to be 9 (the a² term) to complete the square. So, let's add 8 to both sides of the equation to complete the square. This gives us:
   x² + 6x + 9 = 8
4. Factoring the perfect square on the left-hand side, we end up with:
   (x + 3)² = 8
   Since we want to find the zeros, we must now take the square root of both sides to further isolate x.
5. Taking the square root of both sides gives us:
   x + 3 = ±√8
   Remember that we must have a ± whenever we take the square root of a number.
6. Now we subtract 3 from both sides of the equation to finish isolating x. This gives us x = -3 ±√8.
7. The zeros of the equation are x = -3 + √8 and x = -3 - √8.