What is an Inflection Point?

An inflection point is a point along a curve where the curve changes concavity. In other words, the point where the curve (function) changes from concave down to concave up, or concave up to concave down is considered an inflection point. Check out the figures below for a visual reference:

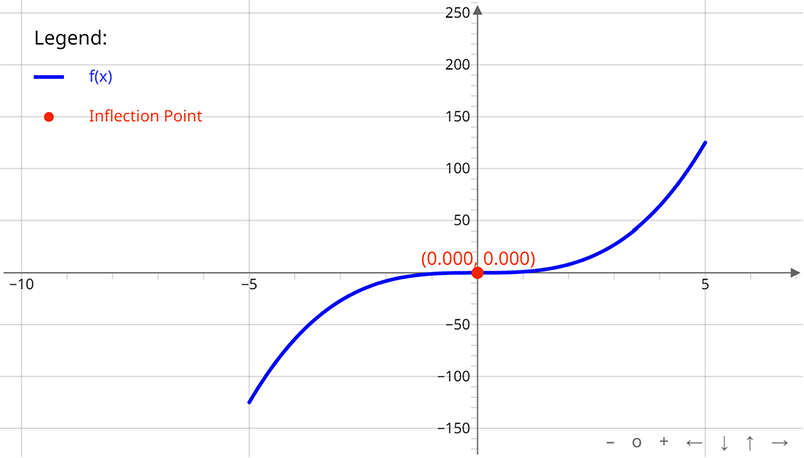
As you can see in Figure 1, the curve changes from concave down to concave up at x = 0, meaning there is an inflection point at this x value.

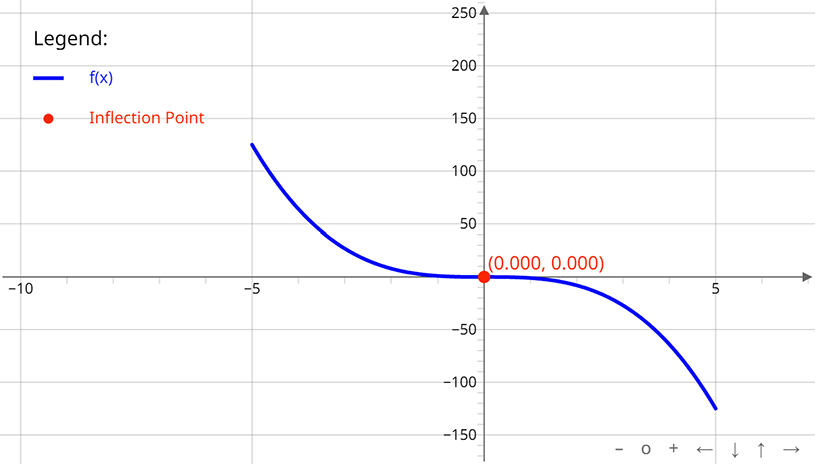
The curve in Figure 2 changes from concave up to concave down at x = 0, also meaning there is an inflection point at this x value.

Why do we Learn About Inflection Points?

Contrary to what one might think, inflection points are useful for more than just passing a math test or completing a homework assignment. Inflection points are found in all sorts of everyday activities like driving, running a business, and even understanding social media trends!

Speaking of social media trends, let's explore how inflection points are useful when growing a social media following.

Let's say that you want to grow a following on a social media platform by creating short-form videos based on a particular trend that has grown in popularity over the recent weeks.

Starting with zero followers, you begin to see rapid growth in your follower count as people discover your content due to its relevancy to the current trend. However, as time progresses, you notice that the rate at which you're gaining followers is starting to decrease. This is an inflection point because the followers vs. time curve changes from concave up to concave down (Figure 3, Point A).

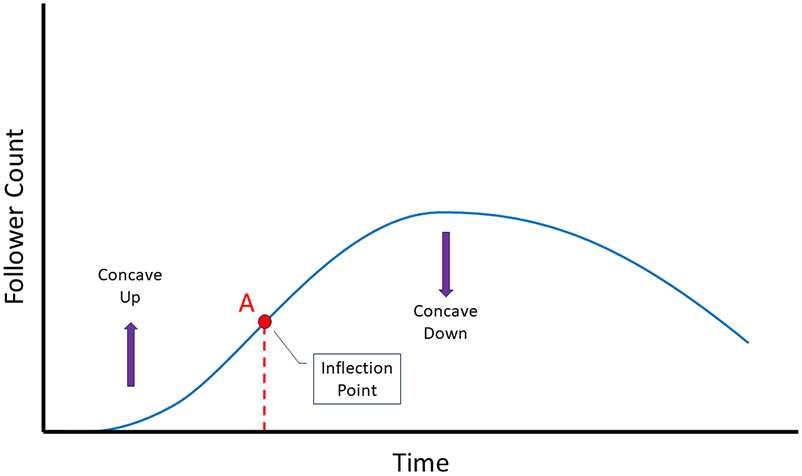
In fact, if you were to continue producing the same type of content for the same trend, your follower count might eventually stop increasing. Or even worse, your follower count could actually go down as time goes on (cue dramatic music).

To prevent this from happening, you could create new videos based on newer, more relevant trends in an attempt to induce an inflection point that causes the curve to change back to being concave up (Figure 4, Point B).

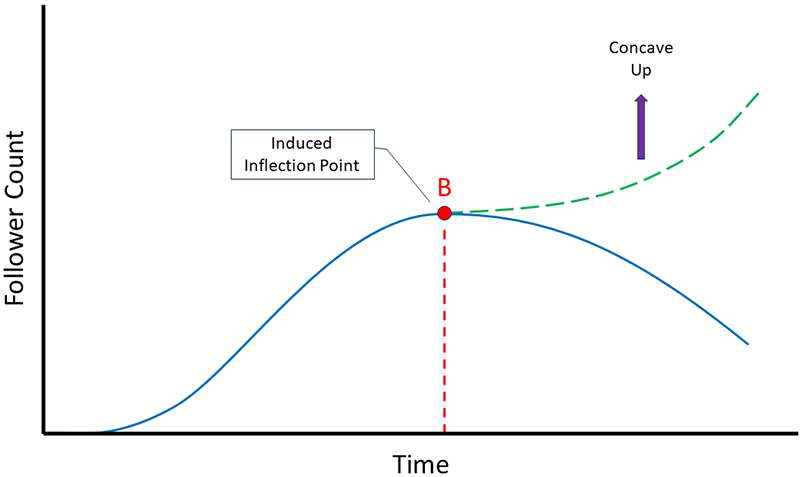
In effect, this would increase the rate at which you would gain followers due to the more relevant content recapturing the viewer's attention and reaching a broader audience. If you think about it, many of your favorite content creators may have taken this same approach, whether it was a conscious effort or not.

Who knew that a concept like inflection points would show up in such a fun and creative space like content creation?!

How to Find Inflection Points

To find the inflection points of a function, follow this process:

1. Take the derivative of f(x) to get f'(x).
2. Take the derivative of f'(x) to get f''(x).
3. Find the x values where f''(x) = 0 OR where f''(x) is undefined. We will refer to these x values as our provisional inflection points (c).
4. Verify that the function f(x) exists at each c value found in Step 3. If the function does not exist at a particular c value, the corresponding c value can be discarded.
5. Perform a concavity test for each remaining c value. This is done by plugging a number just to the left and right of each c value into f''(x) and evaluating whether the sign of the result is positive (concave up) or negative (concave down).
6. Using the concavity results from Step 5, determine if the concavity changes at each remaining c value. In other words, if the sign of the value of f''(x) changes at x = c, that particular c value is an inflection point.

Inflection Point Example Problem

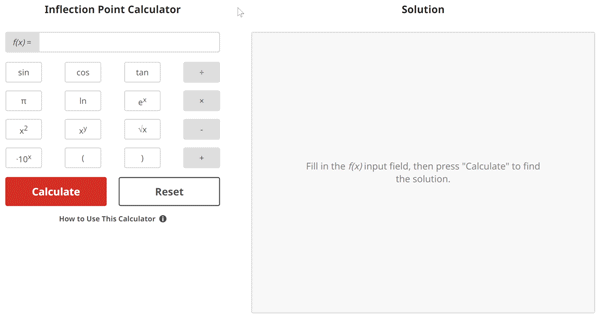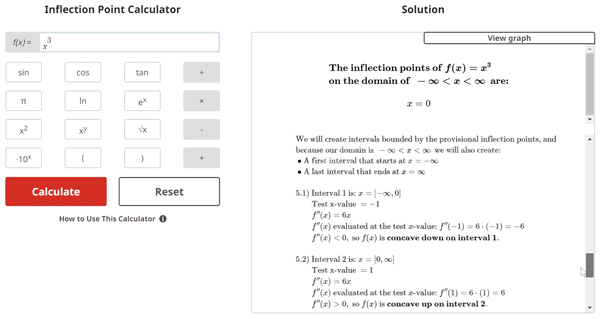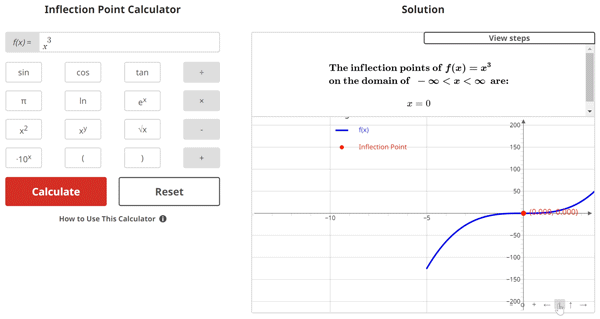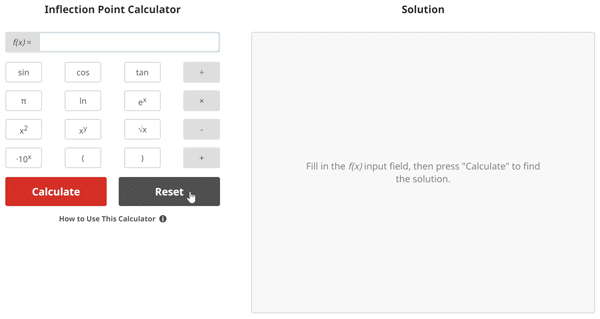
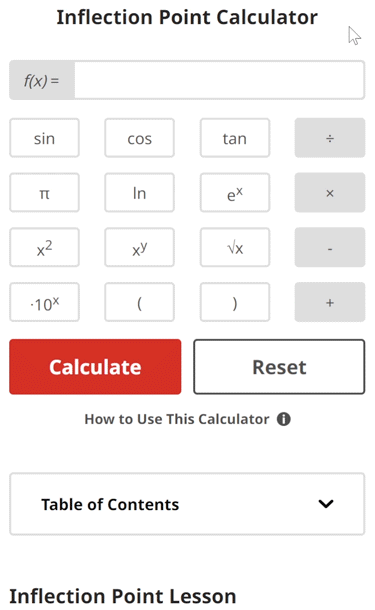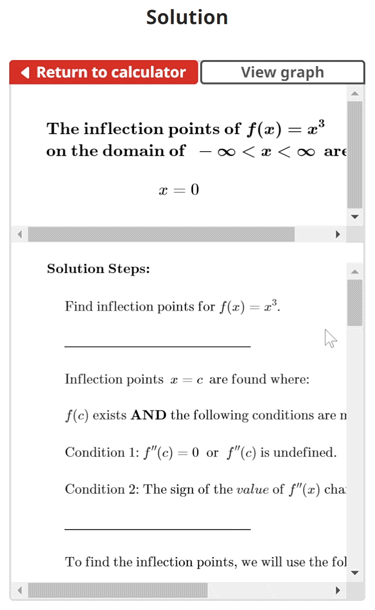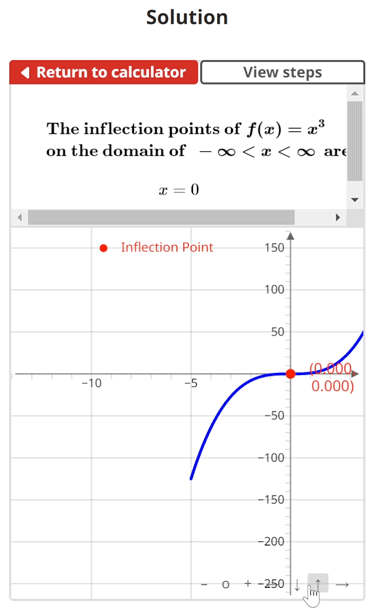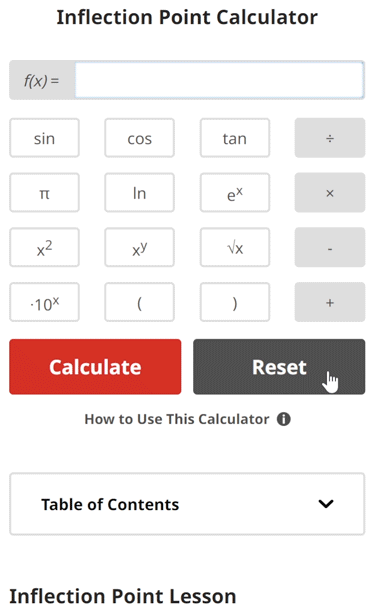
$$\begin{align}& \textbf{Solution Steps:} \hspace{62ex} \\ \\ & \hspace{3ex} \text{Find inflection points for } f(x) = x^3\text{.} \\ \\ & \hspace{3ex} \rule{6cm}{0.8pt} \\ \\ & \hspace{3ex} \text{Inflection points } \: x = c \: \text{ are found where:} \\ \\ & \hspace{3ex} f(c) \text{ exists} \textbf{ AND } \text{the following conditions are met:} \\ \\ & \hspace{3ex} \text{Condition 1: } f''(c) = 0 \; \text{ or } \; f''(c) \text{ is undefined.} \\ \\ & \hspace{3ex} \text{Condition 2: The sign of the } value \text{ of } f''(x) \text{ changes at } x=c \text{.} \\ \\ & \hspace{3ex} \rule{6cm}{0.8pt} \\ \\ & \hspace{3ex} \text{To find the inflection points, we will use the following process:} \\ \\ & \hspace{3ex} \text{Step 1: Take the derivative of } f(x) \text{ to get } f'(x) \text{.} \\ \\ & \hspace{3ex} \text{Step 2: Take the derivative of } f'(x) \text{ to get } f''(x) \text{.} \\ \\ & \hspace{3ex} \text{Step 3: Find the } x \text{ values where } f''(x)=0 \text{ or where } f''(x) \text{ is undefined. We} \\ & \hspace{10.5ex} \text{will refer to these } x \text{ values as our provisional inflection points (} c \text{).} \\ \\ & \hspace{3ex} \text{Step 4: Verify that the function } f(x) \text{ exists at each } c \text{ value found in Step 3. If} \\ & \hspace{10.5ex} \text{the function does not exist at a particular } c \text{ value, the corresponding } c \\ & \hspace{10.5ex} \text{value can be discarded.} \\ \\ & \hspace{3ex} \text{Step 5: Perform a concavity test for each remaining } c \text{ value. This is done by} \\ & \hspace{10.5ex} \text{plugging a number just to the left and right of each } c \text{ value into } f''(x) \\ & \hspace{10.5ex} \text{and evaluating whether the sign of the result is positive (concave up)} \\ & \hspace{10.5ex} \text{or negative (concave down).} \\ \\ & \hspace{3ex} \text{Step 6: Using the concavity results from Step 5, determine if the concavity} \\ & \hspace{10.5ex} \text{changes at each remaining } c \text{ value. In other words, if the sign of the} \\ & \hspace{10.5ex} \text{value of } f''(x) \text{ changes at } x=c \text{, that particular } c \text{ value is an inflection} \\ & \hspace{10.5ex} \text{point.} \\ \\ & \hspace{3ex} \text{Now, let's apply these steps to your function below:} \\ \\ & \hspace{3ex} \rule{6cm}{0.8pt}\\ \\ & \hspace{3ex} \text{1.) First, let's take the derivative of } f(x) \text{ to get } f'(x) \text{:} \\ \\ & \hspace{6.5ex} \Longrightarrow f'(x) = 3 {x}^{2}\\ \\ & \hspace{3ex} \text{2.) Next, let's take the derivative of } f'(x) \text{ to get } f''(x) \text{:} \\ \\ & \hspace{6.5ex} \Longrightarrow f''(x) = 6 x\\ \\ & \hspace{3ex} \text{3.) Now that we have found } f''(x) \text{, let's find where } f''(x) = 0 \text{ or where } f''(x) \\ & \hspace{6.5ex} \text{is undefined to get provisional inflection points (} c \text{):} \\ \\ & \hspace{6.5ex} \Longrightarrow f''(x) = 6 x = 0 \\ \\ & \hspace{6.5ex} \Longrightarrow \text{After solving for } x \text{, we get } x = 0\\ \\ & \hspace{6.5ex} \Longrightarrow c = 0\\ \\ & \hspace{3ex} \text{You're doing great! Now, let's check to make sure that our function } f(x) \text{ exists} \\ & \hspace{3ex} \text{at our provisional inflection }\text{point}\text{ (} c \text{).}\\ \\ & \hspace{3ex} \text{4.) Plugging our } c \text{ value(s) into } f(x) \text{ to get } f(c) \text{, we get:}\\ \\ & \hspace{6.5ex} \Longrightarrow f(c_{1}) = (0)^3 = 0\hspace{1ex} \checkmark \\ \\ & \hspace{11.5ex} \text{Since } f(x) \text { exists at } c_{1}, \text{ we will perform a concavity test at } c_{1} \text{ = } 0\\ & \hspace{11.5ex} \text{in Step 5.} \\\\ \\ & \hspace{3ex} \text{5.) To test for concavity, we will evaluate the derivative } f''(x) \text{ at a} \\ & \hspace{6.5ex} \text{test } x \text{ value } anywhere \; between \text{ each provisional inflection point.} \\ \\ & \hspace{6.5ex} \text{We will create intervals bounded by the provisional inflection points, and} \\ & \hspace{6.5ex} \text{because our domain is} \hspace{1ex} - \infty < x < \infty \hspace{1ex} \text{we will also create:} \\ & \hspace{6.5ex} \bullet \text{A first interval that starts at } x = -\infty \\ & \hspace{6.5ex} \bullet \text{A last interval that ends at } x = \infty\\ \\ & \hspace{6.5ex} \text{5.1) Interval }1\text{ is: } x = [-\infty, 0] \\ & \hspace{11ex} \text{Test x-value } = -1\\ & \hspace{11ex} f''(x) = 6 x\\ & \hspace{11ex} f''(x) \text{ evaluated at the test } x \text{-value: } f''(-1) = 6 \cdot (-1) = -6\\ & \hspace{11ex} f''(x) <0, \text{ so } f(x) \text{ is } \textbf{concave down on interval 1} \text{.}\\ \\ & \hspace{6.5ex} \text{5.2) Interval }2\text{ is: } x = [0, \infty] \\ & \hspace{11ex} \text{Test x-value } = 1\\ & \hspace{11ex} f''(x) = 6 x\\ & \hspace{11ex} f''(x) \text{ evaluated at the test } x \text{-value: } f''(1) = 6 \cdot (1) = 6\\ & \hspace{11ex} f''(x) >0, \text{ so } f(x) \text{ is } \textbf{concave up on interval 2} \text{.}\\ \\ & \hspace{3ex} \text{6.) To find the inflection points, we will look across the intervals for either of} \\ & \hspace{6.5ex} \text{the following two conditions:} \\ \\ & \hspace{6.5ex} \bullet \text{ Condition 1: If } f(x) \text{ changes from concave up (} f''(x) > 0 \text{) over one} \\ & \hspace{22.25ex} \text{interval to concave down (} f''(x) < 0 \text{) over the next interval.} \\ & \hspace{7ex} \text{*OR*} \\ \\ & \hspace{6.5ex} \bullet \text{ Condition 2: If } f(x) \text{ changes from concave down (} f''(x) < 0 \text{) over one} \\ & \hspace{22.25ex} \text{interval to concave up (} f''(x) > 0 \text{) over the next interval.} \\ \\ & \hspace{6.5ex} \text{If either condition is met, there is an inflection point between the} \\ & \hspace{6.5ex} \text{respective intervals.}\\ \\ & \hspace{6.5ex} \text{6.1) Since } f(x) \text{ is } \textbf{concave down} \text{ on interval }1\text{ and is } \textbf{concave up} \text{ on} \\ & \hspace{11ex} \text{interval }2\text{, the } second \; condition \; is \; met \text{. Therefore, there is an} \\ & \hspace{11ex} \text{inflection point at } x = 0\text{.}\\ & \end{align}$$

How the Calculator Works

The Inflection Point Calculator was developed using a combination of HTML (Hypertext Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

HTML can be thought of as the "skeleton", or framework of the calculator. We use this to create and name the actual calculator elements so that the CSS and JS can modify and utilize these elements for visual and functional purposes.

CSS is used to modify the visual appearance of everything from the color of the calculator buttons, to the size of the input field at the top of the calculator.

JS breathes life into the calculator by performing the actual mathematical calculations, displaying the interactive graph, and facilitating useful adaptive features that help the user interact with the web page.

All of these things come together to provide a fast and easy method for learning about inflection points!