Related Content
Z Score Calculator


To get unlimited answers, .
Z-Score Lesson
Lesson Contents
What is the Z-Score?
In statistics, the z-score (also called the standard score) is the number of standard deviations a raw score is from the mean. If the raw score (the observed data point) is greater than the mean (the average of all data points), the z-score will be positive. If the raw score is lesser than the mean, the z-score will be negative.
The z-score formula is given as:
z = (x – μ)⁄σ
Where z is the z-score, x is the raw score, μ is the population mean, and σ is the population standard deviation.
We can also calculate the z-score for a sample of data. To do so, we replace μ with x̄ (the sample mean) and replace σ with S (the sample standard deviation). The resulting z-score formula for a sample of data is given as:
z = (x – x̄)⁄S
Z-Score Example Problem
It is determined that the average weight of all bicycles is 15 kilograms. The population standard deviation is determined to be 2. If a particular bicycle weighs 11 kilograms, what is its z-score?
Solution:
1.) We have all needed values to apply the population z-score formula.
2.) z = (x – μ)⁄σ
z = (11 – 15)⁄2 = -4⁄2 = -2
3.) The z-score of the bicycle’s weight is -2.
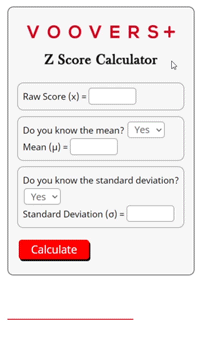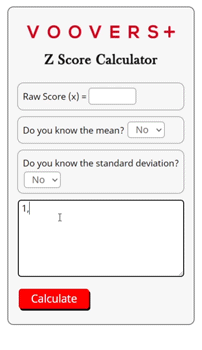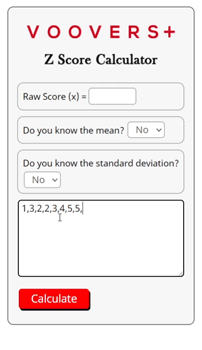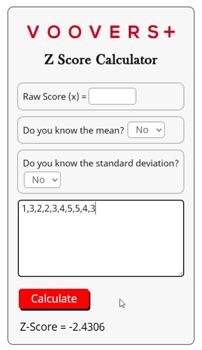
How the Calculator Works
The calculator on this page is written in the programming language JavaScript. When you click the “calculate” button, the zscore function is called and run by your internet browser’s JavaScript engine. Because the browser runs it in real-time without refreshing the page, the answer is calculated and displayed nearly instantly.
At the core of the calculator’s code is the exact z-score formula that was given in the lesson above. The calculator also uses the mean formula and standard deviation formula if those values are not already known and inputted. Once all necessary values are known, they are plugged into the z-score formula.
If any errors on the inputs are detected, an error notice is displayed and calculations are aborted. If a valid solution is computed, it is rounded to the 4th decimal place and displayed as the answer.


