Linear Approximation Calculator
Solution


Linear Approximation Lesson
What is Linear Approximation?
Linear approximation is the process of simplifying a relatively complex function into a linear function that allows us to approximate f(x) when our x value is sufficiently close to a given value x0.
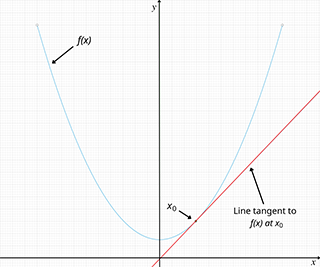
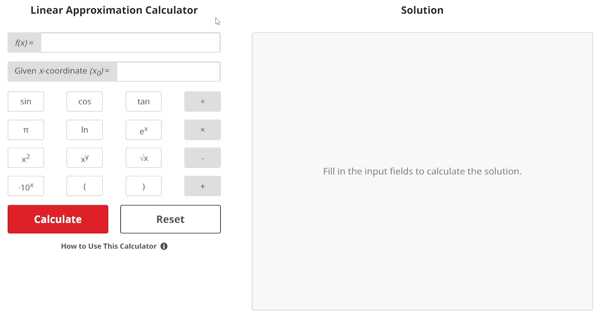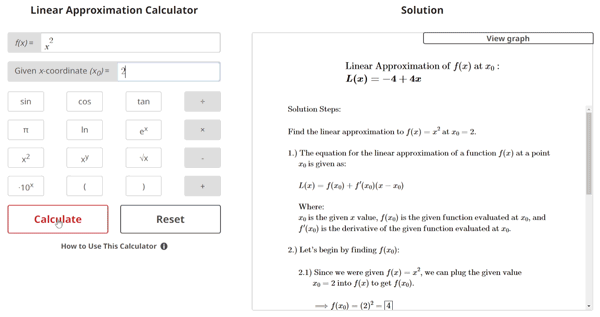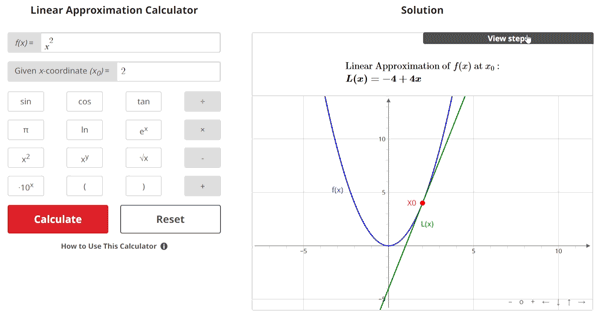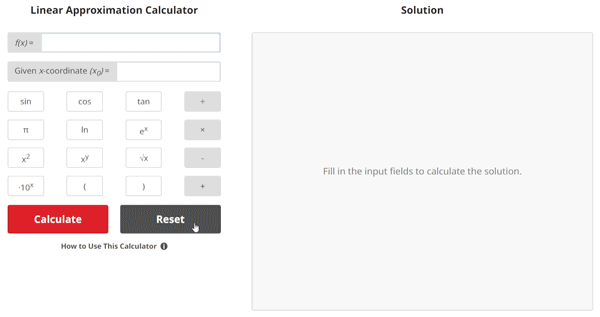
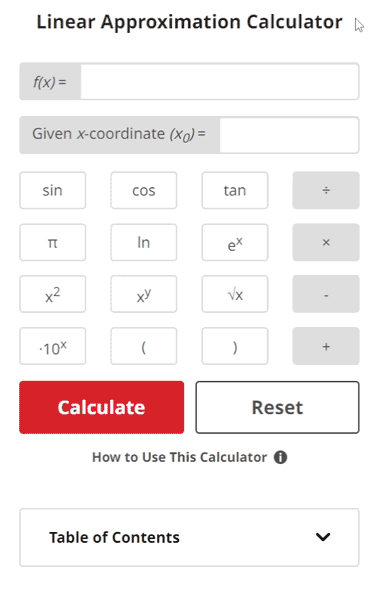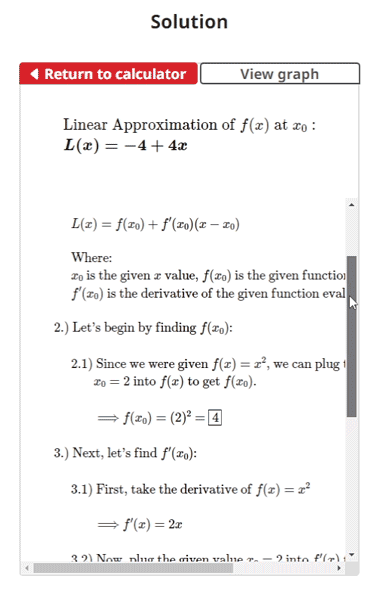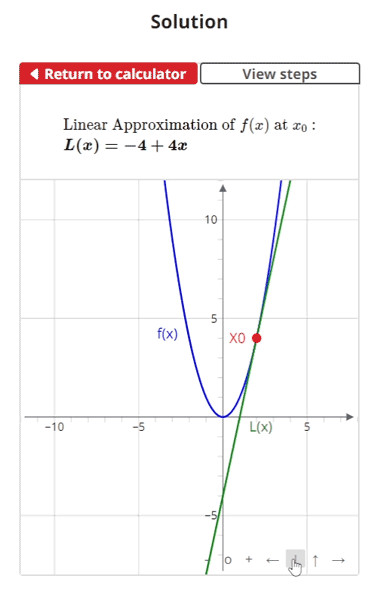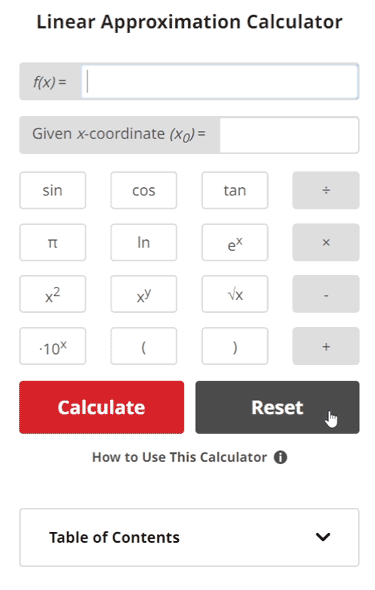
As we zoom in on the point x0, we can see that the curvature of f(x) begins flattening out and looks more like the tangent line (red line).
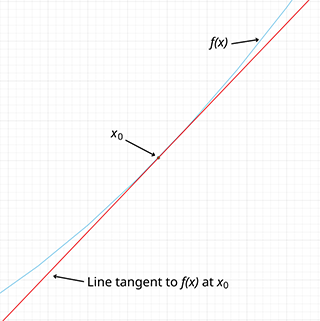
This visualization helps us understand why approximations of f(x) are more accurate near x0. If we keep zooming in on the graph, f(x) will eventually look like a straight line.
While linear approximation is effective at approximating a function near x = x0, the accuracy of the result diminishes as you move farther away from x0. If a higher degree of accuracy is desired, using higher order polynomials via polynomial approximation will generally yield better results when compared to linear approximation.
Why do we Learn About Linear Approximation?
Linear approximation is more than just another topic in a mathematics class. It actually has many practical uses in the real world. One example would be the use of linear approximation to estimate the number of sales a business will make at a point in the near future.
Let's say that you own a growing clothing brand that sells shirts with graphics on them and you want to know how many sales you might expect to see in the near future if business continues growing steadily.

If you know the number of shirts sold over two consecutive years in the past, you can use linear approximation to estimate sales at a later date. Let's check out a basic example below:
Let's say that you sold 350 shirts in 2020. In 2021, you sold 525 shirts. Using the following equation, you can estimate the number of shirts you will sell by the end of 2023.
$$\begin{align} & \text{Estimated Sales(at target year)} = \text{Sales(in 2021)} + \text{Change in Sales(from 2020 to 2021)((target year) - 2021)}\end{align}$$
NOTE: If you compare the above equation to the general equation found in the "How to Linearly Approximate a Function" section below, you can see that they have the same structure.
Plugging in our values we get:
$$\begin{align} & \text{Estimated Sales in 2023} = 525 + (525 \: - \: 350)((2023) \: - \: 2021) \\ \\ & \Longrightarrow \text{Estimated Sales in 2023} = 525 + 175(2) \\ \\ & \Longrightarrow \text{Estimated Sales in 2023} = 875 \text{ shirts}\end{align}$$
Having the ability to simplify relatively complex problems with the use of linear approximation is not only helpful in the sciences, it can also be helpful in business as well!
How to Linearly Approximate a Function
We can linearly approximate a function by using the following equation:
$$\begin{align} & L(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) \hspace{5ex} \textbf{ (1) }\end{align}$$
Where x0 is the given x value, f(x0) is the given function evaluated at x0, and f '(x0) is the derivative of the given function evaluated at x0.
The steps for finding the Linear Approximation of function f(x) are as follows:
- Evaluate f(x) at x0 to get f(x0).
- Take the derivative of f(x) to get f '(x).
- Evaluate f '(x) at x0 to get f '(x0).
- Plug the values obtained from previous steps into the linear approximation equation (Equation 1) and simplify.
Linear Approximation Example Problem
$$\begin{align} & \text{Find the linear approximation to }f(x) = x^2\text{ at } x_{0} = 2.\\ \\ & \text{1.) The equation for the linear approximation of a function } f(x) \text{ at a point} \\ & \hspace{3ex} x_{0} \text{ is given as:} \\ \\ & \hspace{3ex} L(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) \\ \\ & \hspace{3ex} \text{Where: } \\ & \hspace{3ex} x_{0} \text{ is the given } x \text{ value, } f(x_{0}) \text{ is the given function evaluated at } x_{0} \text{, and} \\ & \hspace{3ex} f'(x_{0}) \text{ is the derivative of the given function evaluated at } x_{0} \text{.}\\ \\ & \text{2.) Let's begin by finding } f(x_{0}) \text{:}\\ \\ & \hspace{3ex} \text{2.1) Since we were given } f(x) = x^2\text{, we can plug the given value} \\ & \hspace{7ex} x_{0} = 2\text{ into } f(x) \text{ to get } f(x_{0}) \text{.} \\ \\ & \hspace{7ex} \Longrightarrow f(x_{0}) = {(2)}^{2} = \fbox{4}\\ \\ & \text{3.) Next, let's find } f'(x_{0}) \text{:}\\ \\ & \hspace{3ex} \text{3.1) First, take the derivative of } f(x) = x^2\\ \\ & \hspace{7ex} \Longrightarrow f'(x) = 2 x\\ \\ & \hspace{3ex} \text{3.2) Now, plug the given value } x_{0} = 2\text{ into } f'(x) \text{ to get } f'(x_{0}) \text{.} \\ \\ & \hspace{7ex} \Longrightarrow f'(x_{0}) = 2 (2) = \fbox{4}\\ \\ & \text{4.) Finally, let's plug the values obtained from Steps 2 and 3 into the} \\ & \hspace{3ex} \text{equation for the linear approximation of a function } f(x) \text{ at a point } x_{0} \: \text{:}\\ \\ & \hspace{3ex} \text{4.1) } L(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) \\ \\ & \hspace{7ex} \Longrightarrow L(x) = (4) + (4)(x - (2)) \\ \\ & \hspace{7ex} \Longrightarrow L(x) = -4+4x\\ \\ & \text{Therefore, the linear approximation of } f(x) \text{ at } x_{0} \text{ is:} \\ \\ & \boxed{\boxed{L(x) = -4+4x}}\end{align}$$
How the Calculator Works
The Linear Approximation Calculator is comprised of HTML, CSS, and JS.
HTML stands for "HyperText Markup Language". HTML serves as the framework for the calculator. This allows us to create and name separate entities that will later be styled with CSS or told what to do with JS.
CSS stands for "Cascading Style Sheets". CSS allows us to style various elements by changing their size, shape, color, etc. Everything from the on-screen calculator, to the solution steps fields have been styled using CSS.
JS stands for "JavaScript". JS allows us to add functionality to the calculator. This is what gives the on-screen calculator buttons their functionality, as well as the calculator's ability to perform the calculations required to return a solution to the user.
This all comes together to produce a custom answer, a complete set of detailed of solutions steps, and a helpful graph for the user based on their unique inputs.