Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Variance Calculator
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Variance Lesson
Lesson Contents
Why we Calculate the Variance of a Data Set
Variance is the average squared deviation of each data point from the mean. Calculating the variance gives us an idea of how spread out a data set is around its average value.
The variance equation is the square of the standard deviation equation. Standard deviation is the average amount that each data point deviates from the mean. Since the variance is the square of this, it can make the data appear more spread out than it actually is.
The formula for population variance is given as:
$$\sigma^{2}=\frac{\sum(\mathrm{x}-\mu)^{2}}{\mathrm{N}}$$
And the formula for sample variance is given as:
$$s^{2}=\frac{\sum(x-\bar{x})^{2}}{n-1}$$
We use the population variance formula if the data set represents the entire population and we have access to the population mean. If the data set represents only a sample of the population or don’t have the population mean, we use the sample variance formula.
How the Calculator Works
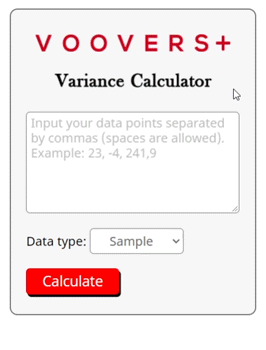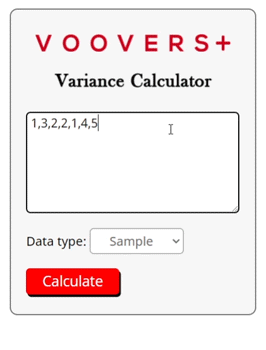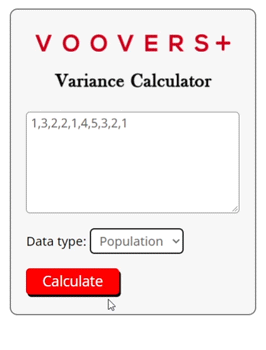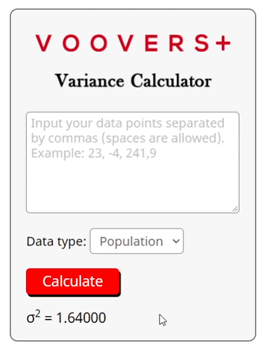
The calculator on this page use a computerized version of the two formulas given above. Your choice of population or sample variance tells the calculator which formula to use. The inputted data set is turned into an array and run through the formula.
The formula spits out the population or sample variance. This answer is then formatted and sent back to this page to be displayed.
