Center of Mass Calculator

What is the Center of Mass?

Have you ever been bored in class or at work and tried to balance a pen, ruler, or other random object on the end of your finger? If this is something you've done before, the concept of the center of mass might be more familiar to you than you think.

The center of mass can be thought of as the balance point for a system of masses located at different distances about a reference point. Mathematically, this ends up being the result when you:

1. Multiply each mass by its relative displacement about a reference point.
2. Add all of the mass-displacement products together.
3. Divide the sum of the mass-displacement products by the sum of the masses.

Why do we Learn About the Center of Mass?

The center of mass is more than just another subject in our math or physics classes. We deal with the realities of this concept often, even when it may not be obvious.

For example, a vehicle's center of mass is relevant when understanding its handling characteristics. Consider two SUV's (Sport Utility Vehicles). One has a conventional internal combustion engine and the other has an all-electric power train with a heavy battery pack located low to the ground within the vehicle.

Assuming the electric vehicle has a lower center of mass compared to the other SUV, the electric vehicle will be able to take turns at a higher rate of speed without tipping because it's center of mass is lower to the ground. The higher the center of mass of a vehicle, the easier it is to tip over.

Automobile manufacturers have even gone as far as designing different engine configurations so that they can be mounted lower in a vehicle to improve handling.

How to Hand Calculate Center of Mass

For a System of Point Masses

A system of point masses is defined as having discrete points that have a known mass. It is an idealized version of real-world systems and helps us simplify center of mass (COM) problems. The COM equation for a system of point masses is given as:

$$\begin{align}\frac{\sum\limits_{i=1}^{n} m_{i}x_{i}}{\sum\limits_{i=1}^{n} m_{i}}\end{align}$$

Where the large Σ means we sum the result of every index i, m_i is the mass of point i, and x_i is the displacement of point i. Displacement is a vector that tells us how far a point is away from the origin and what direction. Positive direction will be positive x and negative direction will be negative x.

By dividing the top summation of all the mass displacement products by the total mass of the system (bottom summation), mass cancels out and we are left with displacement. This displacement will be the distance and direction of the COM.

For Complex Geometries

If we do not have a simple array of discrete point masses in the 1, 2, or 3 dimensions we are working in, finding center of mass can get tricky. Luckily, if we are dealing with a known 2D shape such as a triangle, the centroid of the shape is also the center of mass. There are centroid equations for common 2D shapes that we use as a shortcut to find the center of mass in the vertical and horizontal directions.

If a 2D shape has curved edges, then we must model it using a function and perform a special integral. If it is a 3D shape with curved or smooth outer surfaces, then we must perform a multiple integral. Before integrating, we multiply the integrand by a distance unit. After integrating, we divide by the total area or volume (depending on if it is 2D or 3D shape).

These integral methods calculate the centroid location that is bound by the function and some line or surface. The centroid of a function is effectively its center of mass since it has uniform density and the terms "centroid" and "center of mass" can be used interchangeably. Generally, we will use the term "center of mass" when describing a real, physical system and the term "centroid" when describing a graph or 2-D shape.

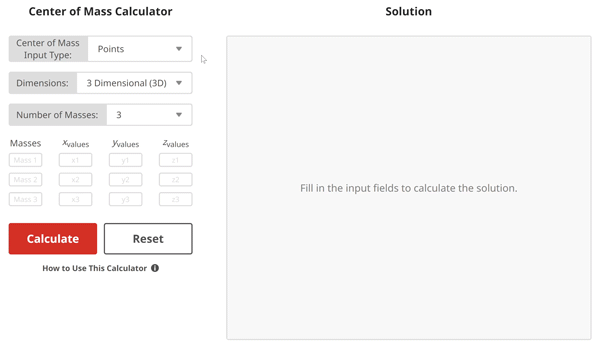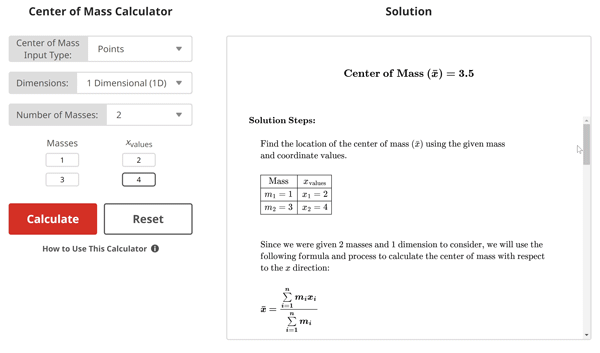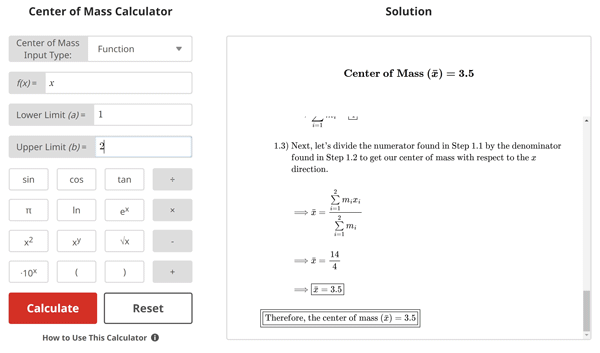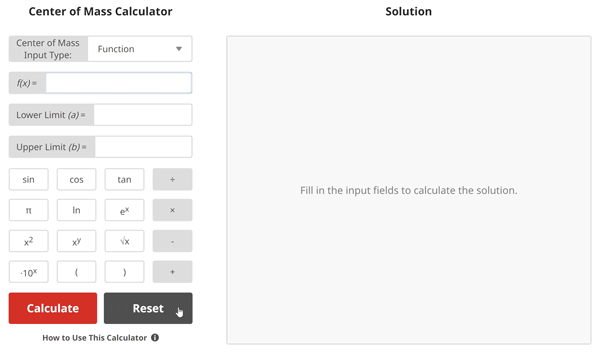
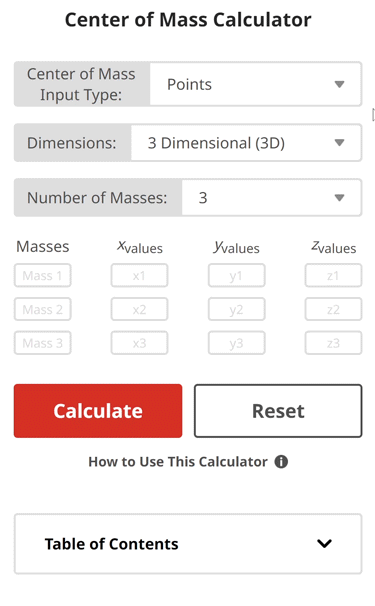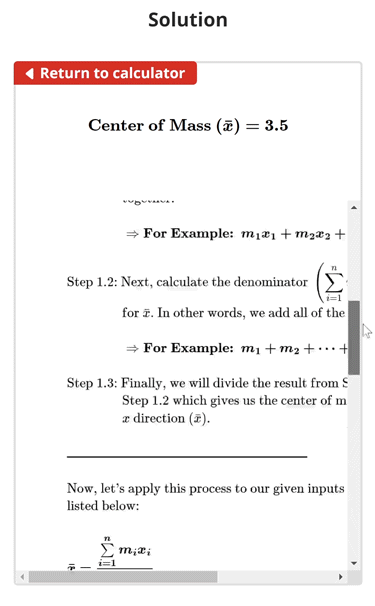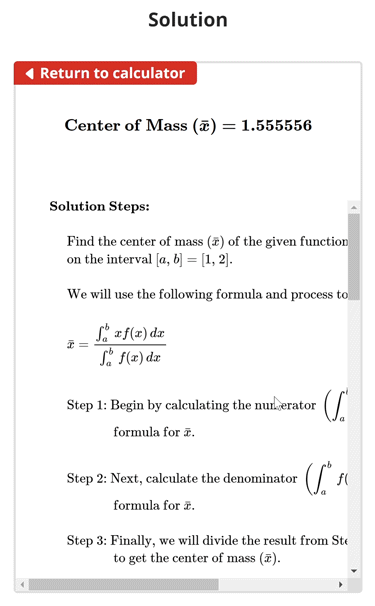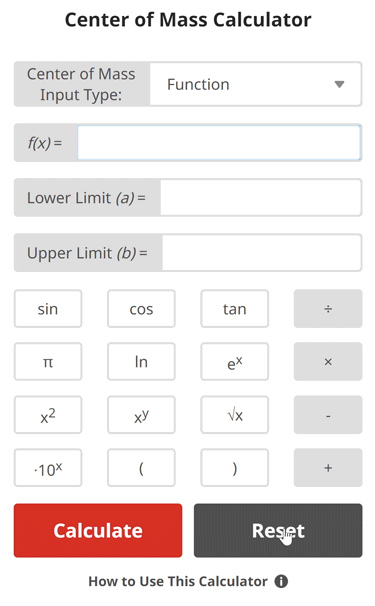
Center of Mass Example Problem (Points)

$$\begin{align}& \textbf{Solution Steps:} \\ \\ & \hspace{3ex} \text{Find the location of the center of mass (}\bar{x}\text{) using the given mass} \\ & \hspace{3ex} \text{and coordinate values.} \\ \\ & \hspace{3ex}\begin{array}{ |c| |c| } \hline \text{Mass} & x_{\text{values}}\\ \hline m_{1} = 1 & x_{1} = 2\\ \hline m_{2} = 3 & x_{2} = 4\\ \hline \end{array}\\ \\ \\ & \hspace{3ex} \text{Since we were given 2 masses and 1 dimension to consider, we will use the} \\ & \hspace{3ex} \text{following }\text{formula}\text{ and process to calculate the center of mass with respect} \\ & \hspace{3ex} \text{to the }x \text{ direction:}\\ \\ & \hspace{3ex} \boldsymbol{\bar{x} = \frac{\sum\limits_{i=1}^{n} m_{i}x_{i}}{\sum\limits_{i=1}^{n} m_{i}}}\\ \\ & \hspace{3ex} \text{Step 1.1: Begin by calculating the numerator } \left(\sum\limits_{i=1}^{n} m_{i}x_{i} \right) \text{ of the given} \\ & \hspace{12.5ex} \text{formula for } \bar{x} \text{.} \text{ Basically, this means that we will multiply each} \\ & \hspace{12.5ex} \text{mass value by its corresponding } x \text{ value and add all of the results} \\ & \hspace{12.5ex} \text{together.} \\ \\ & \hspace{12.5ex} \Rightarrow \textbf{For Example: } \; \boldsymbol{m_{1}x_{1} + m_{2}x_{2} + \cdots + m_{n}x_{n}} \\ \\ & \hspace{3ex} \text{Step 1.2: Next, calculate the denominator } \left(\sum\limits_{i=1}^{n} m_{i} \right) \text{ of the given formula} \\ & \hspace{12.5ex} \text{for } \bar{x} \text{. In other words, we add all of the masses together.} \\ \\ & \hspace{12.5ex} \Rightarrow \textbf{For Example: } \; \boldsymbol{m_{1} + m_{2} + \cdots + m_{n}} \\ \\ & \hspace{3ex}\text{Step 1.3: Finally, we will divide the result from Step 1.1 by the result of} \\ & \hspace{12.5ex} \text{Step 1.2 which gives us the center of mass with respect to the} \\ & \hspace{12.5ex} x \text{ direction (} \bar{x} \text{).}\\ \\ & \hspace {3ex} \rule{8cm}{0.8pt}\\ \\ & \hspace{3ex} \text{Now, let's apply this process to our given inputs using the }\text{formula}\text{ that is} \\ & \hspace{3ex} \text{listed below:} \\ \\ & \hspace{3ex}\boldsymbol{\bar{x} = \frac{\sum\limits_{i=1}^{n} m_{i}x_{i}}{\sum\limits_{i=1}^{n} m_{i}}}\\ \\ & \hspace{3ex} \text{1.) Finding the center of mass with respect to the } x \text{ direction:}\\ \\ & \hspace{6.5ex} \text{1.1) Let's begin by calculating the numerator } \left(\sum\limits_{i=1}^{n} m_{i}x_{i} \right) \text{ where } n = 2\\ & \hspace{11ex} \text{since we have }2\text{ given masses and corresponding coordinate values.} \\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i}x_{i} = m_{1}x_{1} + m_{2}x_{2}\\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i}x_{i} = (1)(2) + (3)(4)\\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i}x_{i} = \boxed{14}\\ \\ & \hspace{6.5ex} \text{1.2) Next, let's calculate the denominator } \left(\sum\limits_{i=1}^{n} m_{i} \right) \text{ where } n = 2\\ & \hspace{11ex} \text{since we have }2\text{ given masses and corresponding coordinate values.} \\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i} = m_{1} + m_{2}\\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i} = (1) + (3)\\ \\ & \hspace{11ex} \Longrightarrow \sum\limits_{i=1}^{2} m_{i} = \boxed{4}\\ \\ & \hspace{6.5ex} \text{1.3) Next, let's divide the numerator found in Step 1.1 by the denominator} \\ & \hspace{11ex} \text{found in Step 1.2 to get our center of mass with respect to the } x \\ & \hspace{11ex} \text{direction.} \\ \\ & \hspace{11ex} \Longrightarrow \bar{x} = \frac{\sum\limits_{i=1}^{2} m_{i}x_{i}}{\sum\limits_{i=1}^{2} m_{i}} \\ \\ & \hspace{11ex} \Longrightarrow \bar{x} = \frac{14}{4} \\ \\ & \hspace{11ex} \Longrightarrow \boxed{\bar{x} = 3.5}\\ \\ & \hspace{3ex} \boxed{\boxed{\text{Therefore, the center of mass }(\bar{x}) = 3.5}}\\ & \end{align}$$

Center of Mass Example Problem (Function)

$$\begin{align}& \textbf{Solution Steps:} \\ \\ & \hspace{3ex} \text{Find the center of mass (} \bar{x} \text{) of the given function } f(x) = x\\ & \hspace{3ex} \text{on the interval [} a \text{, } b \text{]} = \left[1 \text{, }2\right] \text{.} \\ \\ & \hspace{3ex} \text{We will use the following formula and process to calculate the center of mass:} \\ \\ & \hspace{3ex} \bar{x} = \frac{\int_{a}^{b} \, xf(x)\,dx}{\int_{a}^{b} \, f(x)\,dx} \\ \\ & \hspace{3ex} \text{Step 1: Begin by calculating the numerator } \left( \int_{a}^{b} \, xf(x)\,dx \right) \text{ of the given} \\ & \hspace{11ex} \text{formula for } \bar{x} \text{.} \\ \\ & \hspace{3ex} \text{Step 2: Next, calculate the denominator } \left( \int_{a}^{b} \, f(x)\,dx \right) \text{ of the given} \\ & \hspace{11ex} \text{formula for } \bar{x} \text{.} \\ \\ & \hspace{3ex} \text{Step 3: Finally, we will divide the result from Step 1 by the result from Step 2} \\ & \hspace{11ex} \text{to get the center of mass (} \bar{x} \text{).} \\ \\ & \hspace{3ex} \rule{8cm}{0.8pt} \\ \\ & \hspace{3ex} \text{Now, let's apply this process to our given inputs using the formula that is} \\ & \hspace{3ex} \text{listed below:} \\ \\ & \hspace{3ex} \bar{x} = \frac{\int_{a}^{b} \, xf(x)\,dx}{\int_{a}^{b} \, f(x)\,dx}\\ \\ & \hspace{3ex} \text{1.) Let's begin by calculating the numerator } \left( \int_{a}^{b} \, xf(x)\,dx \right) \text{ where} \\ & \hspace{6.5ex} a = 1\; \text{ and } \; b = 2\text{.} \\ \\ & \hspace{6.5ex} \Longrightarrow \int_{a}^{b} \, xf(x)\,dx \\ \\ & \hspace{6.5ex} \Longrightarrow \int_{1}^{2} \, x(x)\,dx \\ \\ & \hspace{6.5ex} \Longrightarrow \int_{1}^{2} \, x^2\,dx \\ \\ & \hspace{6.5ex} \Longrightarrow \left[0.3333333x^3\right]_{1}^{2} \\ \\ & \hspace{6.5ex} \Longrightarrow \left[ 0.3333333\left(2\right)^3\right] - \left[0.3333333\left(1\right)^3\right] \\ \\ & \hspace{6.5ex} \Longrightarrow \left[ 2.666667\right] - \left[0.333333\right] \\ \\ & \hspace{6.5ex} \Longrightarrow \boxed{2.333333}\\ \\ & \hspace{3ex} \text{2.) Next, let's calculate the denominator } \left( \int_{a}^{b} \, f(x)\,dx \right) \text{ where} \\ & \hspace{6.5ex} a = 1\; \text{ and } \; b = 2\text{.} \\ \\ & \hspace{6.5ex} \Longrightarrow \int_{a}^{b} \, f(x)\,dx \\ \\ & \hspace{6.5ex} \Longrightarrow \int_{1}^{2} \, (x)\,dx \\ \\ & \hspace{6.5ex} \Longrightarrow \left[0.5x^2\right]_{1}^{2} \\ \\ & \hspace{6.5ex} \Longrightarrow \left[ 0.5\left(2\right)^2\right] - \left[0.5\left(1\right)^2\right] \\ \\ & \hspace{6.5ex} \Longrightarrow \left[ 2\right] - \left[0.5\right] \\ \\ & \hspace{6.5ex} \Longrightarrow \boxed{1.5}\\ \\ & \hspace{3ex} \text{3.) Next, let's divide the numerator found in Step 1 by the denominator} \\ & \hspace{6.5ex} \text{found in Step 2 to get our center of mass (} \bar{x} \text{).} \\ \\ & \hspace{6.5ex} \Longrightarrow \bar{x} = \frac{\int_{1}^{2} \, xf(x)\,dx}{\int_{1}^{2} \, f(x)\,dx} \\ \\ & \hspace{6.5ex} \Longrightarrow \bar{x} = \frac{2.333333}{1.5} \\ \\ & \hspace{6.5ex} \Longrightarrow \boxed{\bar{x} = 1.555556}\\ \\ & \hspace{3ex} \boxed{\boxed{\text{Therefore, the center of mass (} \bar{x} \text{) } = 1.555556}}\\ & \end{align}$$

How the Calculator Works

The Center of Mass Calculator is comprised of HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

HTML serves as the framework of the calculator. With HTML, we can create the calculator outline, buttons, text, and other entities that the user might interact with.

CSS then changes the appearance of the stock HTML elements. This is what allows us to give the calculator its signature Voovers interface that is responsive across multiple devices.

Once the calculator is on the page and styled, JS is used to make the calculator actually do things. When you press a button on the on-page keypad, JS is used to type the corresponding input into the relevant field. Also, JS is used to perform the actual calculations themselves.

All of these languages work together to create an excellent learning aid for the center of mass.