Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Confidence Interval Calculator
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Confidence Interval Lesson
Lesson Contents
Why do we Calculate a Confidence Interval?
In statistics, we use a confidence interval to predict a range of values that the true mean will be reside in. The chance of the true mean being in this range of values is the “confidence” level of the interval.
For example, we may sample data from 50 people in a population of 100,000 people. We determine the sample mean and standard deviation for a data point of interest. Since we only sampled a small fraction of the entire population that we are concerned with, the sample mean is not an accurate mean for the entire population, which is known as the true mean.
If we calculate the 95% confidence interval for the data, our true mean will have a 95% chance of residing within this interval. As the percentage of the confidence interval goes up, the width of the interval goes up drastically. A 99% confidence interval may be extremely wide/loose in comparison to a 90% confidence interval.
The Limitations of a Confidence Interval: What to Look out for!
The key word in confidence interval is confidence. Statistical predictions give a chance of something being true. A 95% confidence interval translates literally to there being a 95% chance that the true mean is within the interval. There is no guarantee that the true mean will be in the confidence interval. If there was a guarantee, then it would be called a 100% certainty interval.
With confidence intervals, the number of sample data points matters a lot. If the sample size (called n) is 30 or less, we use the t-score. If the sample size is greater than 30 or we know the population standard deviation, we can use the z-score.
Ideally the sample size will be greater than 30 and we will have the standard deviation. This will give us a tighter confidence interval. Greater sample size also gives us a tighter confidence interval.
How the Calculator Works
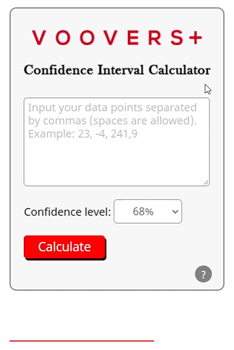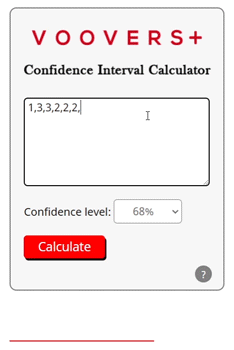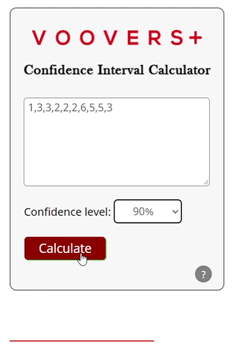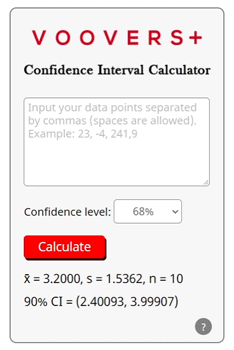
The calculator on this page uses a similar process to how we hand calculate a confidence interval. It calculates the sample mean, sample standard deviation, and n, the number of sample data points. From there, it uses the t/z score equation to calculate the interval halves that flank the sample mean.
Once the interval halves are added and subtracted to and from the sample mean, the interval is formatted into confidence interval notation. That result is sent back to this page and displayed as the answer.
