Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Work Calculator
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Lesson on Work
Lesson Contents
The Definition of Work
In mechanical physics, work is the product of force and displacement. The general formula for work is given as:
W = F×d
Where W is the work, F is the applied force, and d is the displacement. The standard unit for work is the joule (J). Work can be thought of as a transfer of energy or a change of energy state for an object.
When someone or something puts out work, they transfer energy to the object that they did work on. However, not all the energy always goes into the object. In the real world, energy is lost to friction; this can be friction between objects, between fluid molecules, or both.
In idealized physics problems where friction is neglected, work is equal to energy change. An example of this would be an object sitting at ground level on the earth. It has zero gravitational potential energy because it has no height to fall. If we do work on it by lifting it vertically off the ground, its gravitational potential energy will be equal to the work we did on it.
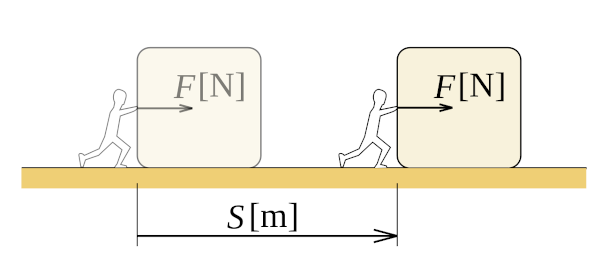
When force that is applied to an object IS in the same direction that it is displaced like shown above, we use the general work equation. If the force applied is NOT in the same direction as the direction that the object is displaced, then the equation for work is given as:
W = F×d×cos(θ)
Where W is work, F is the force applied to the object, θ is the angle between the directions of force application and object displacement, and d is the displacement.
The SI unit of work is the joule, and the U.S. customary unit of work is the foot-pound. These are the same units as energy because work is equal to energy. This relationship, known as the work-energy principle, is very useful when solving problems in classical mechanics.
The equation for the work-energy principle is given as:
W = ∆KE
Where W is the work done on the object and ΔKE is the change in kinetic energy of the object. If the object gains or loses height relative to a gravitational body, then its change in gravitational potential energy should also be considered by adding the gravitational energy component to the equation.
Example Problem
A structural member of a building under construction must be lifted by a crane from the ground to the 20th floor, which is 60 meters above the ground. The object has a mass of 400 kg. How much work must be done on the member to move it from the ground to the 20th floor?
Solution:
1.) Force required to lift = weight of member. Weight of member = (mass)×(gravitational acceleration) = (400 kg)×(9.81 m/s2) = 3,924 N.
2.) Force required to lift = 3,924 N. Recall that W = F×d.
3.) W = (3,924 N)×(60 m) = 235,440 joules.
How the Calculator Works
The calculator on this page uses the same formula that we use when hand calculating work. It takes your input numbers and units, converts the values to standard calculation units (if needed), then computes the work.
Once the work is calculated, it converts to your selected output unit before sending the final answer back to this page along with its respective output unit.
