Angle Between Two Vectors Calculator
Solution


Angle Between Two Vectors Lesson
Overview of the Angle Between two Vectors
A vector is a quantity that has both magnitude and direction. This is often represented by an arrow of a set length (magnitude) that is pointing in a specific direction in two-dimensional or three-dimensional space. The shortest angle in which one of the arrows (vectors) is rotated to match the direction of the other arrow (vector) is known as the angle between two vectors.
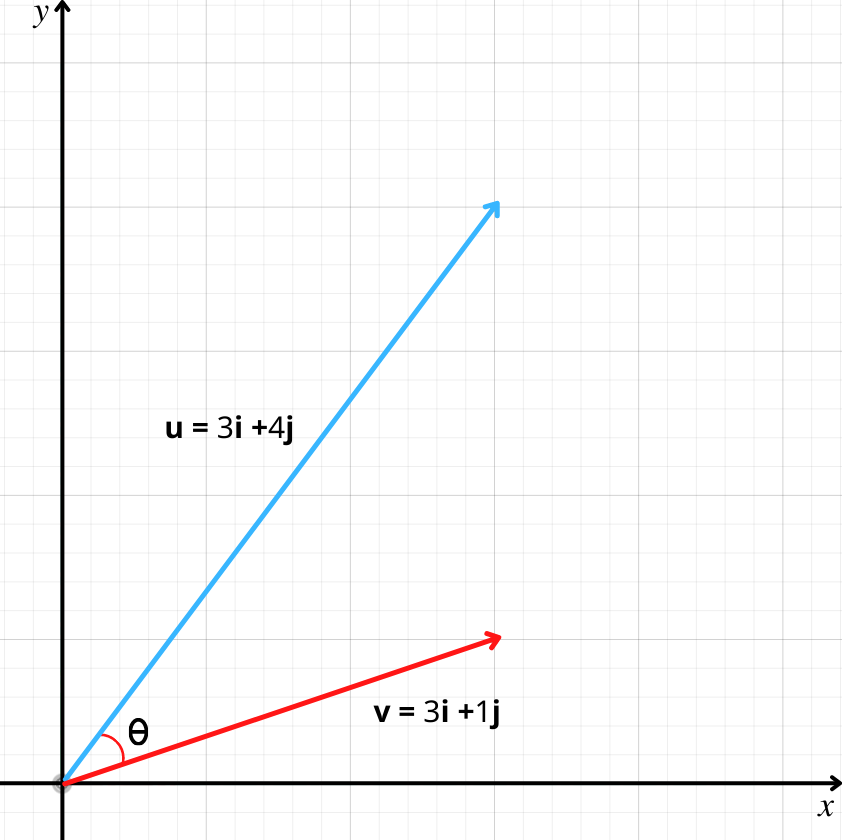
Why do we Learn About the Angle Between two Vectors?
The dot products of vectors and the angles between them can be a useful building block for not only understanding the theoretical relationship between vectors, but also in understanding how these relationships correlate to our lives in a practical or tangible way.
And what could be more tangible than getting into a roller coaster ride vehicle and plummeting down a steep drop?

Let's say that we are designing a new roller coaster and we want to get a basic understanding of some of the ride's characteristics based on the profile of the track and the weight of the ride vehicle. In this case, we want to get an estimation of the work done on the ride vehicle due to gravity when it accelerates down a linear decline.
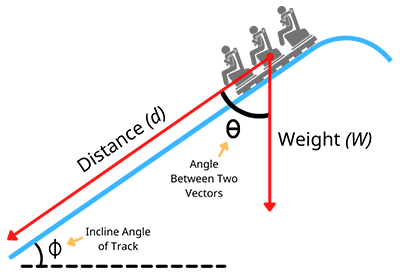
Knowing the weight of the vehicle, the linear distance traveled, and the angle of the track, we can utilize the concept of dot products and the angle between vectors to estimate the work done on the vehicle by the time it reaches the bottom of the drop. This is useful information because we can then anticipate how much energy will need to be taken up by a braking system to stop the vehicle at the end of the drop.
Now, let's take a look at the equation for work and compare it to the equation used to relate the angle between two vectors to the dot product of two vectors:
$$\begin{align} & \text{Work } = F \cdot d = |F| |d| \: cos \: \theta \\ \\ & cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{u} \right| \left| \textbf{v} \right|} \end{align}$$
As you can see, the second equation is a rearranged version of the first one. Now, if we apply the work equation to our example, we get the following:
$$\begin{align} & \text{Work } = W \cdot d = |W| |d| \: cos \: \theta \end{align}$$
This helps us understand the energy requirements for our braking system so that the vehicle can be stopped safely at the end of the drop.
How to Calculate the Angle Between two Vectors
We can calculate the angle between two vectors by using the following equation:
$$\begin{align} & cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{u} \right| \left| \textbf{v} \right|} \hspace{10ex} \textbf{ (1) } \end{align}$$
Where u · v is the dot product of vectors u and v, |u| is the magnitude of vector u, |v| is the magnitude of vector v, and θ is the angle between vectors u and v.
The steps for solving for the angle between two vectors are as follows:
- Compute the dot product u · v.
- Find |u| (magnitude of vector u).
- Find |v| (magnitude of vector v).
- Plug u · v, |u|, and |v| into the equation for finding the angle between two vectors (Equation 1) and solve for θ.
- (Optional) Convert answer to degrees from radians as necessary.
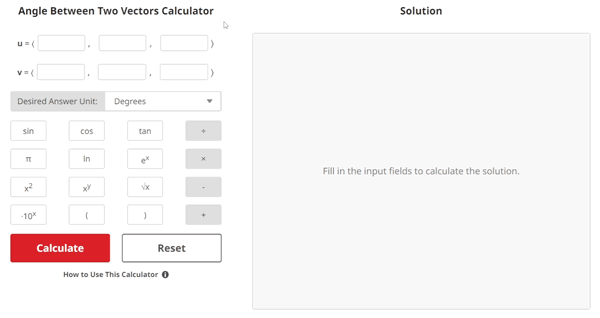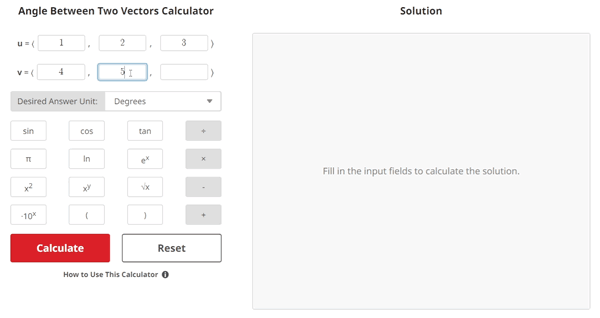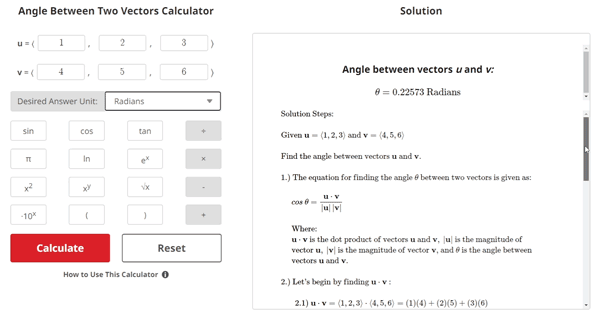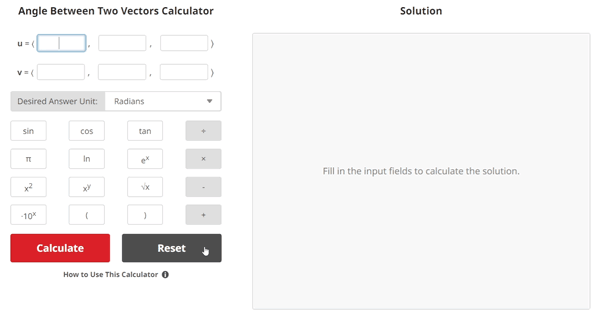
Angle Between Two Vectors Example Problem
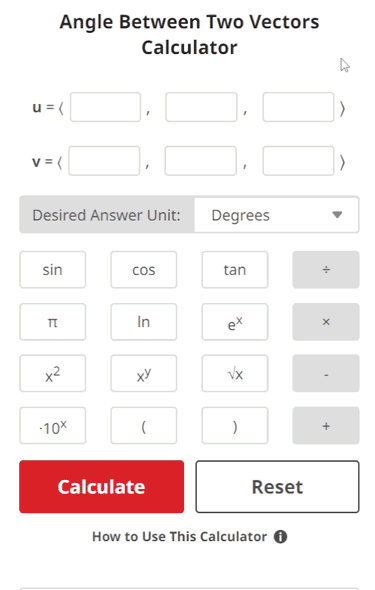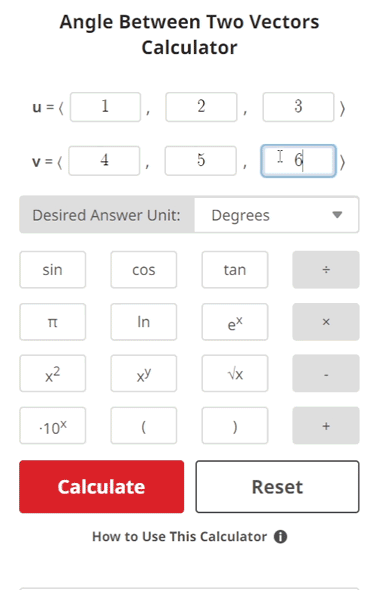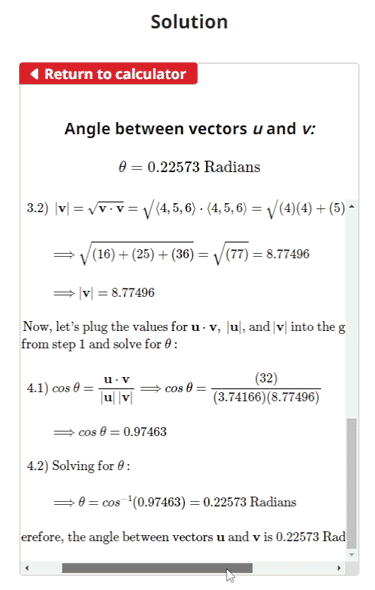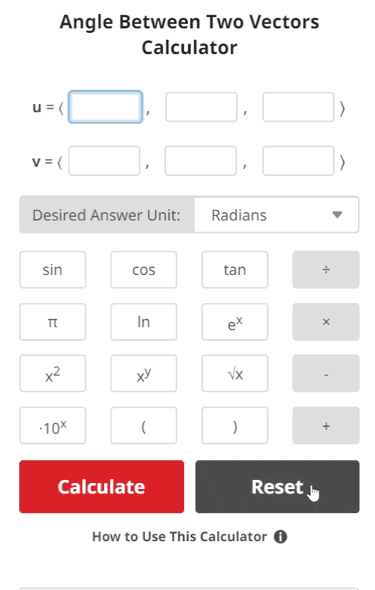
$$\begin{align} & \text{Given:} \\ \\ & \textbf{u} = \langle 1, 2, 3\rangle \text{ and } \textbf{v} = \langle 4, 5, 6\rangle \\ \\ & \text{Find the angle between vectors } \textbf{u} \text{ and } \textbf{v} \text{.}\\ \\ & \text{1.) The equation for finding the angle } \theta \text{ between two vectors is given as:} \\ \\ & \hspace{3ex} cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{u} \right| \left| \textbf{v} \right|} \\ \\ & \hspace{3ex} \text{Where: } \\ & \hspace{3ex} \textbf{u} \cdot \textbf{v} \text{ is the dot product of vectors } \textbf{u} \text{ and } \textbf{v} \text{, } \left| \textbf{u} \right| \text{ is the magnitude of } \\ & \hspace{3ex} \text{vector } \textbf{u} \text{, } \left| \textbf{v} \right| \text{ is the magnitude of vector } \textbf{v} \text{, and } \theta \text{ is the angle between} \\ & \hspace{3ex} \text{vectors } \textbf{u} \text{ and } \textbf{v} \text{.}\\ \\ & \text{2.) Let's begin by finding } \textbf{u} \cdot \textbf{v} \: \text{:}\\ \\ & \hspace{4ex} \text{2.1) } \textbf{u} \cdot \textbf{v} = \langle1, 2, 3\rangle \cdot \langle 4, 5, 6\rangle = (1)(4) + (2)(5) + (3)(6) \\ \\ & \hspace{8ex} \Longrightarrow (4) + (10) + (18) = 32\\ \\ & \hspace{8ex} \Longrightarrow \textbf{u} \cdot \textbf{v} = 32\\ \\ & \text{3.) Next, let's find} \left| \textbf{u} \right| \text{ and} \left| \textbf{v} \right| \: \text{:}\\ \\ & \hspace{4ex} \text{3.1) } \left| \textbf{u} \right| = \sqrt{\textbf{u} \cdot \textbf{u}} = \sqrt{\langle1, 2, 3\rangle \cdot \langle1, 2, 3\rangle} = \sqrt{(1)(1) + (2)(2) + (3)(3)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(1) + (4) + (9)} = \sqrt{(14)} = 3.74166\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{u} \right| = 3.74166\\ \\ & \hspace{4ex} \text{3.2) } \left| \textbf{v} \right| = \sqrt{\textbf{v} \cdot \textbf{v}} = \sqrt{\langle4, 5, 6\rangle \cdot \langle4, 5, 6\rangle} = \sqrt{(4)(4) + (5)(5) + (6)(6)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(16) + (25) + (36)} = \sqrt{(77)} = 8.77496\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{v} \right| = 8.77496\\ \\ & \text{4.) Now, let's plug the values for } \textbf{u} \cdot \textbf{v} \text{, } \left| \textbf{u} \right| \text{, and} \left| \textbf{v} \right| \text{ into the given equation} \\ & \hspace{3ex} \text{from step 1 and solve for } \theta \: \text{:}\\ \\ & \hspace{4ex} \text{4.1) } cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{u} \right| \left| \textbf{v} \right|} \Longrightarrow cos \: \theta = \frac{(32)}{(3.74166)(8.77496)} \\ \\ & \hspace{8ex} \Longrightarrow cos \: \theta = 0.97463\\ \\ & \hspace{4ex} \text{4.2) Solving for } \theta \: \text{:} \\ \\ & \hspace{8ex} \Longrightarrow \theta = cos^{-1}(0.97463) = 0.22573\text{ Radians}\\ \\ & \text{5.) Finally, let's convert angle } \theta \text{ from radians to degrees:}\\ \\ & \hspace{4ex} \text{5.1) } \theta = (0.22573 \text{ Radians}) \cdot (\frac{\text{180 Degrees}}{\pi \text{ Radians}}) = 12.93315^{\circ}\\ \\ & \text{Therefore, the angle between vectors } \textbf{u} \text{ and } \textbf{v} \text{ is }12.93315^{\circ} \text{.}\end{align}$$
How the Calculator Works
The Angle Between Two Vectors Calculator is comprised of several programming languages. These languages include HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).
HTML is used to create the basic framework of the calculator and solution fields. These fields are given special identifiers that are referenced when the calculator elements are being styled, when special operations are being carried out during the calculation, and when the dropdown menu for the answer unit selection is used.
CSS is used to apply styling characteristics to the HTML elements referenced above. This includes, but is not limited to, the shape, size, and color of the calculator and solution fields.
JS is what gives the calculator its actual functionality. When you click a button on the calculator or press "calculate", the JS code starts designating actions that lead to the desired end result. For example, when you click the "+" button on the keypad, the JS tells the calculator to add the "+" character in the desired input field for you. Similarly, when you press calculate, JS tells the calculator to perform a prescribed set of operations that leads to a custom answer and set of solution steps based on your question.
All of these different languages come together to deliver an easy-to-use, effective, and satisfying learning experience.