Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Gravitational Force Calculator
Mass 1 (m1):
Mass 2 (m2):
Distance (r):
Force (F) =
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Lesson on Universal Gravitation
Lesson Contents
How to Calculate the Force of Gravity
Newton’s law of universal gravitation tells us that every particle in the universe attracts every other particle in the universe with a force called gravity. We can apply this concept to objects that we know the mass of and distance between.
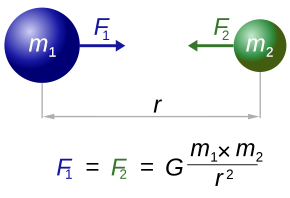
The formula for finding the force of gravity between two objects is given as:
F = Gm1m2⁄r2
Where F is the attractive force between the objects, G is the gravitational constant, m1 is the mass of object 1, m2 is the mass of object 2, and r is the distance between the objects.
The gravitational constant G has been researched extensively since its discovery. As of 2018, the most recent and accurate value for it is 6.6743×10-11 N-m2⁄kg2.
To calculate the gravitational force between two objects, we simply plug the two objects’ masses, the distance between them, and the gravitational constant into the formula given above. The formula provides us the attractive force in newtons (N).
How the Calculator Works
The calculator on this page is written in the programming language JavaScript (abbreviated as JS). When an input to one of the textboxes or unit drop-down boxes is detected, the function gravity is run by your internet browser’s JS engine. The browser’s built-in JS engine allows the calculator to provide near-instant results.
The code itself is very simple. First, it converts the inputted numbers to the standard units used in the universal gravitation formula. Then, it applies the same force formula as given in the lesson above. The answer is converted to the desired output units (such as kN or GN). That answer is rounded to the 4th decimal place and displayed as the solution.
The calculator also has built-in error handling. If it detects any inputs that are either invalid or could cause calculation errors, it bypasses the calculations. The next time an input change is detected, it checks all inputs again and either performs the calculations or bypasses them.
