Related Content
Law of Cosines Calculator

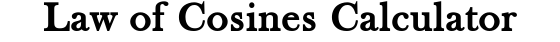
To get unlimited answers, .
Law of Cosines Lesson
Lesson Contents
What is the Law of Cosines?
The law of cosines is a set of formulas that relate the side lengths of a triangle with the cosines of its angles. It allows us to solve for unknown side lengths and angles of any triangle if we know two of the side lengths and one of the angles.
The three law of cosines formulas are given as:
a2 = b2 + c2 – 2bc×cos(A)
b2 = a2 + c2 – 2ac×cos(B)
c2 = a2 + b2 – 2ab×cos(C)
Where a, b, and c are the side lengths and A, B, and C are the angles opposite of their respective side. For example, angle A is opposite to side a and located between sides b and c
The law of cosines is a one-size-fits-all version of the Pythagorean theorem. The Pythagorean theorem has a much simpler formula but only works with right triangles. The law of cosines works with any type of triangle.
How to Hand Calculate with the Law of Cosines
To solve a triangle by hand with the law of cosines, we first determine which sides and angles are already known.
Then, we pick one of the three formulas to start with. We may rearrange the formula to either solve for a side length or an angle.
Plugging in the known values and then reducing and simplifying the equation, we will end up with the isolated parameter. Then we may repeat the process to solve for other sides or angles.
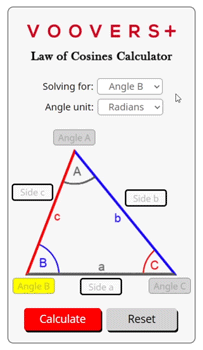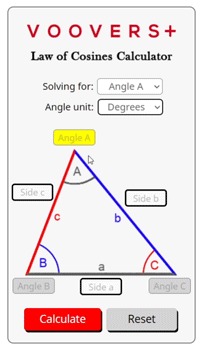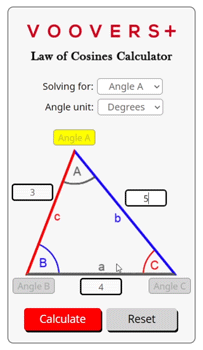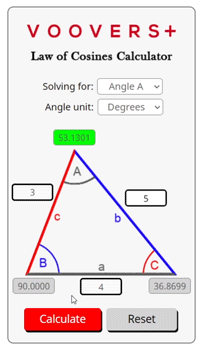
How the Calculator Works
The calculator on this page is written in the programming language JavaScript. When you click the “calculate” button, the law of cosines function is activated. This function is run by your internet browser’s JavaScript engine which allows nearly instant answers.
At the core of the code powering this calculator are the same formulas as given above. Your inputted side lengths and angle are fed into the applicable formula, and out comes the desired side length or angle value. That resulting number is rounded to the 4th decimal place before being displayed as the answer.
The code also checks the side lengths and angles of your triangle to make sure that it follows the triangle inequality theorem and that no internal angles exceed 180 degrees. If the sides and angles do not constitute a possible triangle then no answer will be calculated.


