Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Implicit Differentiation Calculator
=
Solve for:
Solution:
1.1) ...
Voovers+ Full Solution Steps Preview:
$$\begin{align}& \hspace{2ex} \text{Solution Steps:} \\ \\ & \hspace{2ex} \text{Find } \: \frac{dy}{dx} \left[e^x-x^2y^2=5+yx^2\right]\\ \\ & \hspace{2ex} \text{To do this, we will:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Differentiate each side of the equation with respect to }x\\ & \hspace{5ex} \text{AND with respect to }y\text{ as an implicit (implied) function of }x\\ & \hspace{5ex} \text{while adding } \frac{dy}{dx} \text{ to terms where }y\text{ was differentiated} \\ \\ & \hspace{3ex} \text{2) Algebraically rearrange the equation so all } \frac{dy}{dx} \text{ operators} \\ & \hspace{5ex} \text{are isolated on one side of the equation as a single } \frac{dy}{dx}\\ \\ & \text{1.1) To differentiate the left side of the equation with respect to }x\\ & \hspace{4ex} \text{and with respect to }y\text{ as an implicit (implied) function of }x\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dx} \text{ of the entire left side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dy}{dx} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }y\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[e^x-x^2y^2\right] \: \Longrightarrow \:{e}^{x}-2 x {y}^{2}-2 {x}^{2} y\frac{dy}{dx}\\ \\ & \hspace{4ex}\text{Since term }3\text{ resulted from the variable }y\text{ being differentiated,} \\ & \hspace{4ex} \text{we have added a } \frac{dy}{dx} \text{ operator to it.}\\ \\ & \text{1.2) To differentiate the right side of the equation with respect to }x\\ & \hspace{4ex} \text{and with respect to }y\text{ as an implicit (implied) function of }x\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dx} \text{ of the entire right side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dy}{dx} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }y\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[5+yx^2\right] \: \Longrightarrow \:2 x y+{x}^{2}\frac{dy}{dx}\\ \\ & \hspace{4ex}\text{Since term }2\text{ resulted from the variable }y\text{ being differentiated,} \\ & \hspace{4ex} \text{we have added a } \frac{dy}{dx} \text{ operator to it.}\\ \\ & \text{2.1) We will now begin isolating the } \frac{dy}{dx} \text{ operators. First, let's combine} \\ & \hspace{4ex} \text{our resultant equation sides from step 1 back into a single equation.} \\ \\ & \hspace{4ex} \text{Left side } = \text{ Right side} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[e^x-x^2y^2\right] = \frac{d}{dx} \left[5+yx^2\right] \\ \\ & \hspace{6ex} \Longrightarrow \; {e}^{x}-2 x {y}^{2}-2 {x}^{2} y\frac{dy}{dx}=2 x y+{x}^{2}\frac{dy}{dx}\\ \\ & \text{2.2) Now we will move all terms with a } \frac{dy}{dx} \text{ to the left side of the equation} \\ & \hspace{4ex} \text{and all terms without a } \frac{dy}{dx} \text{ to the right side of the equation.} \\ \\ & \hspace{4ex}{e}^{x}-2 x {y}^{2}-2 {x}^{2} y\frac{dy}{dx}=2 x y+{x}^{2}\frac{dy}{dx}\\ \\ & \hspace{6ex} \Longrightarrow \; -2 {x}^{2} y\frac{dy}{dx}-{x}^{2}\frac{dy}{dx}=2 x y-{e}^{x}+2 x {y}^{2}\\ \\ & \text{2.3) Next, let's factor out the } \frac{dy}{dx} \text{ from the left side terms.} \\ \\ & \hspace{4ex}-2 {x}^{2} y\frac{dy}{dx}-{x}^{2}\frac{dy}{dx}=2 x y-{e}^{x}+2 x {y}^{2}\\ \\ & \hspace{6ex} \Longrightarrow \; \frac{dy}{dx} \left(-2 {x}^{2} y-{x}^{2}\right)=2 x y-{e}^{x}+2 x {y}^{2}\\ \\ & \text{2.4) Finally, we will divide the entire right side by the quantity on} \\ & \hspace{4ex} \text{the left side to finish isolating } \frac{dy}{dx} \text{ and get our final answer.} \\ \\ & \hspace{4ex}\frac{dy}{dx} \left(-2 {x}^{2} y-{x}^{2}\right)=2 x y-{e}^{x}+2 x {y}^{2}\\ \\ & \hspace{6ex} \Longrightarrow \; \boxed{\boxed{ \frac{dy}{dx} = \frac{2 x y-{e}^{x}+2 x {y}^{2}}{-2 {x}^{2} y-{x}^{2}}}}\end{align}$$
Implicit Differentiation Lesson
Lesson Contents
What is Implicit Differentiation?
Implicit differentiation is the process of finding the derivative of an implicit function.
Typically, we take derivatives of explicit functions, such as y = f(x) = x2. This function is considered explicit because it is explicitly stated that y is a function of x.
Sometimes though, we must take the derivative of an implicit function. For example, 5xy2 = 2x – 12y is considered to be implicit because it is implied that y is a function of x, rather than being explicitly stated.
Implicit differentiation allows us to find a derivative with respect to either variable we choose, which means we can take dy⁄dx or dx⁄dy of an implicit function like 5xy2 = 2x – 12y.
This is because we may choose to consider y to be an implicit function of x or may choose to consider x to be an implicit function of y.
Why do we Learn About Implicit Differentiation?
In general, derivates are extensively used in real-world science and engineering applications. But when must we take the derivative of an implicit function in real life? One of the many examples of this is to design a high-performance race engine’s rotating assembly so it can withstand the loads it will experience during operation.
A Honda V10 Formula 1 Engine
This is because an engine’s rotating assembly is made up of three main components: the crankshaft (colored blue in the image below), the connecting rod (colored red in the image below), and the piston (shaded with black lines in the image below).
In a race engine such as the Honda V10 Formula 1 Engine pictured above, the connecting rod experiences enormous loads due to combustion pressure and inertial forces of the entire rotating assembly moving at very high velocities and rates of acceleration.
The Motion Pattern of a Piston Engine Throughout the Combustion Cycle
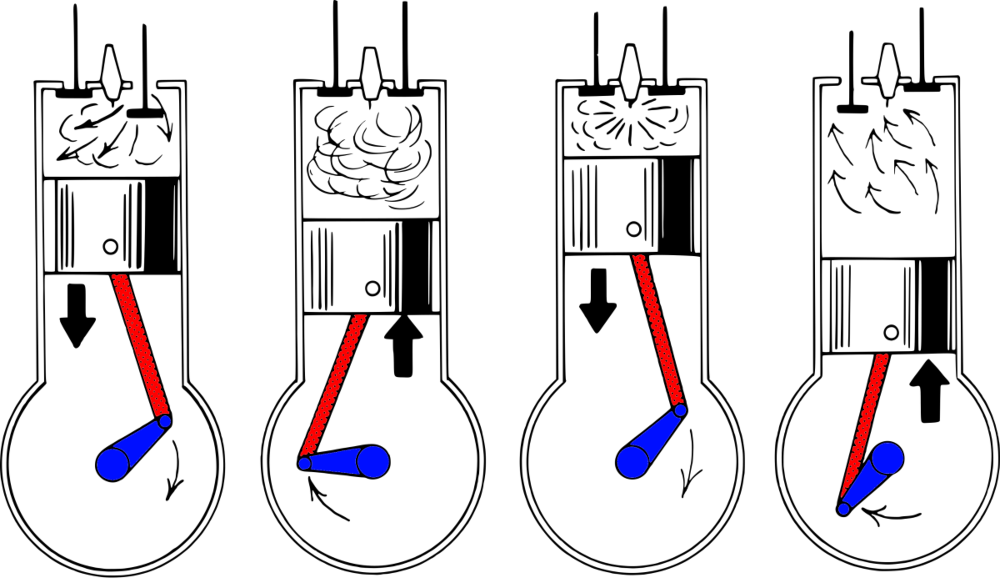
Fortunately, we can model the connecting rod’s position with an implicit function that relates the angle of the crankshaft and connecting rod respectively.
By performing implicit differentiation on the implicit function that models the position, we find the function that defines the connecting rod’s velocity. We can again differentiate this velocity function to get the acceleration function.
With these functions now known, we can easily calculate the forces the connecting rod must withstand during operation and design the rod to reliably operate without structural failure.
How to Solve an Implicit Differentiation Problem
How to find dy⁄dx using implicit differentiation:
1.) Differentiate each side of the equation with respect to x AND with respect to y as an implicit (implied) function of x. Add a dy⁄dx operator to terms where y was differentiated.
→ For example, the term 2xy would be differentiated with respect to x, resulting in 2y. It is also differentiated with respect to y as an implicit (implied) function of x, resulting in 2xdy⁄dx. The total result from 2xy is 2y + 2xdy⁄dx.
2.) Now that both sides of the equation are differentiated, algebraically rearrange the equation so that all dy⁄dx operators are isolated as a single dy⁄dx on the left side of the equation.
2.1) Combine the left side and right side results back into a single equation, such that the left side results = the right side results.
2.2) Then, move all terms with a dy⁄dx to the left side of the equation, and all terms without a dy⁄dx to the right side of the equation.
2.3) Now that the terms with dy⁄dx are isolated on the left side of the equation, factor the dy⁄dx out of the terms. The left side of the equation will now have a single dy⁄dx multiplied by a quantity of terms.
2.4) Finally, divide the entire right side of the equation by the quantity of terms on the left side of the equation. This leaves a single dy⁄dx isolated on the left side of the equation and results in the final answer.
How to find dx⁄dy using implicit differentiation:
1.) Differentiate each side of the equation with respect to y AND with respect to x as an implicit (implied) function of y. Add a dx⁄dy operator to terms where x was differentiated.
→ For example, the term 2yx would be differentiated with respect to y, resulting in 2x. It is also differentiated with respect to x as an implicit (implied) function of y, resulting in 2ydx⁄dy. The total result from 2yx is 2x + 2ydx⁄dy.
2.) Now that both sides of the equation are differentiated, algebraically rearrange the equation so that all dx⁄dy operators are isolated as a single dx⁄dy on the left side of the equation.
2.1) Combine the left side and right side results back into a single equation, such that the left side results = the right side results.
2.2) Then, move all terms with a dx⁄dy to the left side of the equation, and all terms without a dx⁄dy to the right side of the equation.
2.3) Now that the terms with dx⁄dy are isolated on the left side of the equation, factor the dx⁄dy out of the terms. The left side of the equation will now have a single dx⁄dy multiplied by a quantity of terms.
2.4) Finally, divide the entire right side of the equation by the quantity of terms on the left side of the equation. This leaves a single dx⁄dy isolated on the left side of the equation and results in the final answer.
Example Problem 1
$$\begin{align}& \hspace{2ex} \text{Find } \: \frac{dy}{dx} \left[x^2y-2x+\frac{5}{y}-5=0\right]\\ \\ & \hspace{2ex} \text{To do this, we will:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Differentiate each side of the equation with respect to }x\\ & \hspace{5ex} \text{AND with respect to }y\text{ as an implicit (implied) function of }x\\ & \hspace{5ex} \text{while adding } \frac{dy}{dx} \text{ to terms where }y\text{ was differentiated} \\ \\ & \hspace{3ex} \text{2) Algebraically rearrange the equation so all } \frac{dy}{dx} \text{ operators} \\ & \hspace{5ex} \text{are isolated on one side of the equation as a single } \frac{dy}{dx}\\ \\ & \text{1.1) To differentiate the left side of the equation with respect to }x\\ & \hspace{4ex} \text{and with respect to }y\text{ as an implicit (implied) function of }x\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dx} \text{ of the entire left side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dy}{dx} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }y\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[x^2y-2x+\frac{5}{y}-5\right] \: \Longrightarrow \:2 x y+{x}^{2}\frac{dy}{dx}-2-\frac{5}{{y}^{2}}\frac{dy}{dx}\\ \\ & \hspace{4ex}\text{Since terms }2\text{ and }4\text{ resulted from the variable }y\text{ being differentiated,} \\ & \hspace{4ex} \text{we have added } \frac{dy}{dx} \text{ operators to them.}\\ \\ & \text{1.2) To differentiate the right side of the equation with respect to }x\\ & \hspace{4ex} \text{and with respect to }y\text{ as an implicit (implied) function of }x\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dx} \text{ of the entire right side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dy}{dx} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }y\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[0\right] \: \Longrightarrow \:0\\ \\ & \hspace{4ex}\text{Since no terms resulted from the variable }y\text{ being differentiated,} \\ & \hspace{4ex} \text{we have not added any } \frac{dy}{dx} \text{ operators.}\\ \\ & \text{2.1) We will now begin isolating the } \frac{dy}{dx} \text{ operators. First, let’s combine} \\ & \hspace{4ex} \text{our resultant equation sides from step 1 back into a single equation.} \\ \\ & \hspace{4ex} \text{Left side } = \text{ Right side} \\ \\ & \hspace{4ex} \frac{d}{dx} \left[x^2y-2x+\frac{5}{y}-5\right] = \frac{d}{dx} \left[0\right] \\ \\ & \hspace{6ex} \Longrightarrow \; 2 x y+{x}^{2}\frac{dy}{dx}-2-\frac{5}{{y}^{2}}\frac{dy}{dx}=0\\ \\ & \text{2.2) Now we will move all terms with a } \frac{dy}{dx} \text{ to the left side of the equation} \\ & \hspace{4ex} \text{and all terms without a } \frac{dy}{dx} \text{ to the right side of the equation.} \\ \\ & \hspace{4ex}2 x y+{x}^{2}\frac{dy}{dx}-2-\frac{5}{{y}^{2}}\frac{dy}{dx}=0\\ \\ & \hspace{6ex} \Longrightarrow \; {x}^{2}\frac{dy}{dx}-\frac{5}{{y}^{2}}\frac{dy}{dx}=-2 x y+2\\ \\ & \text{2.3) Next, let’s factor out the } \frac{dy}{dx} \text{ from the left side terms.} \\ \\ & \hspace{4ex}{x}^{2}\frac{dy}{dx}-\frac{5}{{y}^{2}}\frac{dy}{dx}=-2 x y+2\\ \\ & \hspace{6ex} \Longrightarrow \; \frac{dy}{dx} \left({x}^{2}-\frac{5}{{y}^{2}}\right)=-2 x y+2\\ \\ & \text{2.4) Finally, we will divide the entire right side by the quantity on} \\ & \hspace{4ex} \text{the left side to finish isolating } \frac{dy}{dx} \text{ and get our final answer.} \\ \\ & \hspace{4ex}\frac{dy}{dx} \left({x}^{2}-\frac{5}{{y}^{2}}\right)=-2 x y+2\\ \\ & \hspace{6ex} \Longrightarrow \; \boxed{\boxed{ \frac{dy}{dx} = \frac{-2 x y+2}{{x}^{2}-\frac{5}{{y}^{2}}}}}\end{align}$$
Example Problem 2
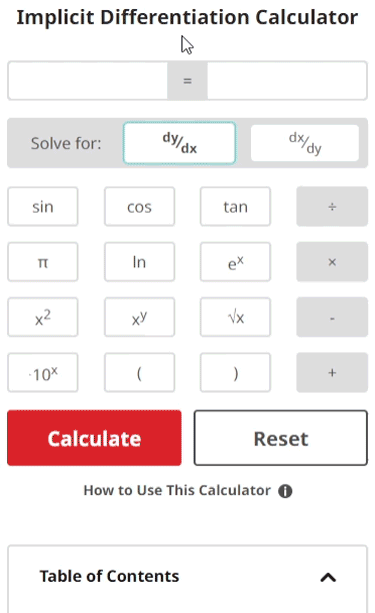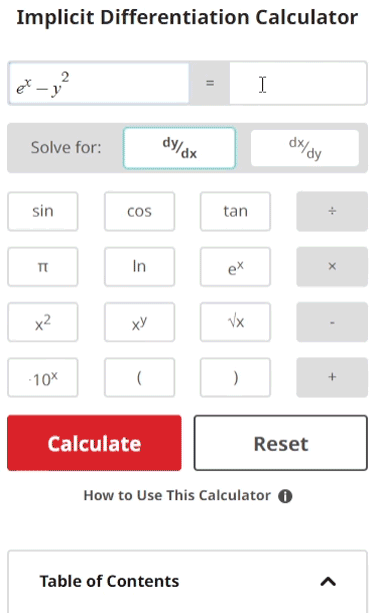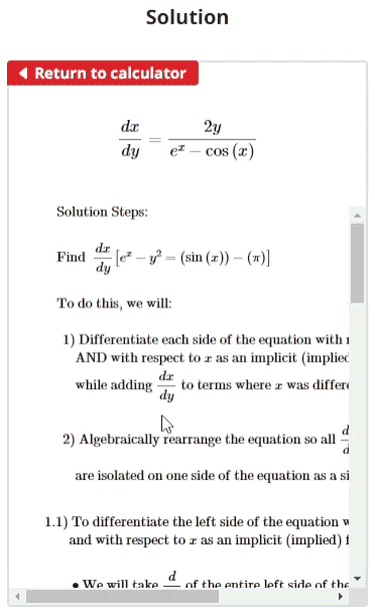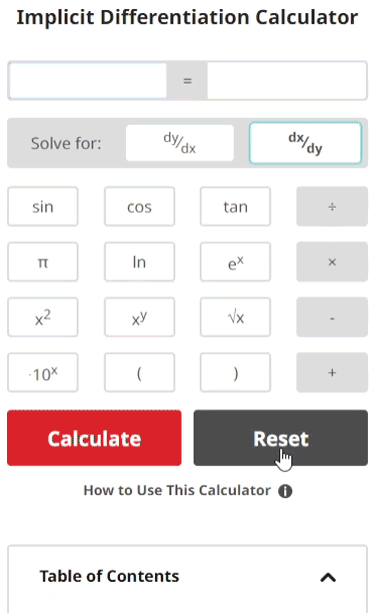
$$\begin{align}& \hspace{2ex} \text{Find } \: \frac{dx}{dy} \left[e^x-y^2=\sin\left(x\right)-\pi\right]\\ \\ & \hspace{2ex} \text{To do this, we will:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Differentiate each side of the equation with respect to }y\\ & \hspace{5ex} \text{AND with respect to }x\text{ as an implicit (implied) function of }y\\ & \hspace{5ex} \text{while adding } \frac{dx}{dy} \text{ to terms where }x\text{ was differentiated} \\ \\ & \hspace{3ex} \text{2) Algebraically rearrange the equation so all } \frac{dx}{dy} \text{ operators} \\ & \hspace{5ex} \text{are isolated on one side of the equation as a single } \frac{dx}{dy}\\ \\ & \text{1.1) To differentiate the left side of the equation with respect to }y\\ & \hspace{4ex} \text{and with respect to }x\text{ as an implicit (implied) function of }y\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dy} \text{ of the entire left side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dx}{dy} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }x\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dy} \left[e^x-y^2\right] \: \Longrightarrow \:{e}^{x}\frac{dx}{dy}-2 y\\ \\ & \hspace{4ex}\text{Since term }1\text{ resulted from the variable }x\text{ being differentiated,} \\ & \hspace{4ex} \text{we have added a } \frac{dx}{dy} \text{ operator to it.}\\ \\ & \text{1.2) To differentiate the right side of the equation with respect to }y\\ & \hspace{4ex} \text{and with respect to }x\text{ as an implicit (implied) function of }y\text{:} \\ \\ & \hspace{4ex} \bullet \text{We will take } \frac{d}{dy} \text{ of the entire right side of the equation} \\ & \hspace{4ex} \bullet \text{We will also add a } \frac{dx}{dy} \text{ to terms that resulted from} \\ & \hspace{6ex} \text{the variable }x\text{ being differentiated} \\ \\ & \hspace{4ex} \frac{d}{dy} \left[\sin\left(x\right)-\pi\right] \: \Longrightarrow \:\mathrm{cos}\left(x\right)\frac{dx}{dy}\\ \\ & \hspace{4ex}\text{Since term }1\text{ resulted from the variable }x\text{ being differentiated,} \\ & \hspace{4ex} \text{we have added a } \frac{dx}{dy} \text{ operator to it.}\\ \\ & \text{2.1) We will now begin isolating the } \frac{dx}{dy} \text{ operators. First, let’s combine} \\ & \hspace{4ex} \text{our resultant equation sides from step 1 back into a single equation.} \\ \\ & \hspace{4ex} \text{Left side } = \text{ Right side} \\ \\ & \hspace{4ex} \frac{d}{dy} \left[e^x-y^2\right] = \frac{d}{dy} \left[\sin\left(x\right)-\pi\right] \\ \\ & \hspace{6ex} \Longrightarrow \; {e}^{x}\frac{dx}{dy}-2 y=\mathrm{cos}\left(x\right)\frac{dx}{dy}\\ \\ & \text{2.2) Now we will move all terms with a } \frac{dx}{dy} \text{ to the left side of the equation} \\ & \hspace{4ex} \text{and all terms without a } \frac{dx}{dy} \text{ to the right side of the equation.} \\ \\ & \hspace{4ex}{e}^{x}\frac{dx}{dy}-2 y=\mathrm{cos}\left(x\right)\frac{dx}{dy}\\ \\ & \hspace{6ex} \Longrightarrow \; {e}^{x}\frac{dx}{dy}-\mathrm{cos}\left(x\right)\frac{dx}{dy}=2 y\\ \\ & \text{2.3) Next, let’s factor out the } \frac{dx}{dy} \text{ from the left side terms.} \\ \\ & \hspace{4ex}{e}^{x}\frac{dx}{dy}-\mathrm{cos}\left(x\right)\frac{dx}{dy}=2 y\\ \\ & \hspace{6ex} \Longrightarrow \; \frac{dx}{dy} \left({e}^{x}-\mathrm{cos}\left(x\right)\right)=2 y\\ \\ & \text{2.4) Finally, we will divide the entire right side by the quantity on} \\ & \hspace{4ex} \text{the left side to finish isolating } \frac{dx}{dy} \text{ and get our final answer.} \\ \\ & \hspace{4ex}\frac{dx}{dy} \left({e}^{x}-\mathrm{cos}\left(x\right)\right)=2 y\\ \\ & \hspace{6ex} \Longrightarrow \; \boxed{\boxed{ \frac{dx}{dy} = \frac{2 y}{{e}^{x}-\mathrm{cos}\left(x\right)}}}\end{align}$$
How the Calculator Works
This calculator is built upon three web programming technologies: HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).
The HTML code builds out the calculator’s architecture and provides the framework for all things we see and click when interacting with it.
The CSS code defines the calculator’s styling, including but not limited to its shape, color, and button movement.
The JS code provides all functionality for the calculator. It detects inputs, clicks, and has an entire routine that is run when a calculation is called for. The JS calculation routine is very similar to the implicit differentiation process that is taught in this lesson. And, throughout the routine, snapshots of the problem are taken and later used as the solution steps that we see.
