Related Content
Triple Integral Calculator

To get unlimited answers, .

Triple Integral Lesson
Lesson Contents
What does a Triple Integral Actually Calculate?
The above calculator finds the solution to your definite triple integral within the x, y, and z integration limits that you inputted. Calculating a triple integral allows us to find the volume contained within of a 3-d shape. The difference between a triple and a double integral is that double integrals find the volume under a surface, whereas a triple integral finds the volume between two continuous surfaces that comprise a shape.
One of the most difficult parts of calculating triple integrals is visualizing it and then setting up the limits of integration. To understand how to set up and calculate the integral, it is important to understand how calculus operations are able to calculate volume of a 3D shape. In the next section we will explain the process.
How to Solve Triple Integrals
We perform triple integrals on functions of three variables. Just like a double integral, we solve triple integrals by iterated integrals. Pictured below is the notation of a definite triple integral.
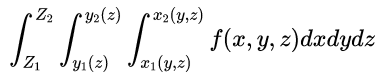
As we can see, the triple integral ends up being three iterated integrals in which the order is determined by how the notation is set up. The iterated integrals are performed from innermost to outermost. In this case, the order goes dx, then dy, then dz. The limits of integration for each variable are ordered to match dx, dy, and dz.
The limits of integration are written as functions of the limits to their outside because of the iterated nature of a triple integral. Using the image above as an example, dx is integrated first so the result of that remains a function of y and z. After dy, it remains a function of z.
How the Triple Integral Calculator Works
The calculator on this page computes your triple integral symbolically by using a computer algebra system. In symbolic integration, the computer algebra system uses algebra and integral rules to take the antiderivative of the function before applying the fundamental theorem of calculus. In fact, it iterates through the integral just as described in the section above. In essence, symbolic integration follows the same steps as a human with a paper and pencil would. It has the capability to attain near perfect solution accuracy. The calculator on this page is accurate to a minimum of the 5th decimal place!
The alternative to using symbolic integration to solve triple integrals is called numerical integration. A numerical integration routine performs a relatively small and approximated version of the problem as many times as necessary to converge to an accurate solution. Generally, numerical routines can solve a greater range of problems but can take longer and potentially be less accurate.


