What is a Double Integral?

A double integral is a multiple integral of a function of two variables. It is called a double integral because we must perform a definite integral two times (one for each of the two variables).

To further our understanding, let's compare single integrals and double integrals:

• The single integral of a function of one variable such as y = f(x) solves for the area under the function's 2-dimensional curve.
• A double integral of a function of two variables such as z = f(x, y) solves for the volume under the function's 3-dimensional surface.

A double integral for a function f(x, y) may be notated as:

$$\begin{align} & \int \limits_{y_{1}}^{y_{2}} \int \limits_{x_{1}}^{x_{2}} f(x, y) \; dx\hspace{1pt} dy \end{align}$$

Where x₁ is the lower x limit of integration, x₂ is the upper x limit of integration, y₁ is the lower y limit of integration, y₂ is the upper y limit of integration, f(x, y) is a function of x and y, dx indicates integration of the variable x, and dy indicates integration of the variable y.

Why do we Learn How to do Double Integrals?

Double integrals have many, many applications in the world of engineering, science, and statistics. But, let's hone in on just one of these applications: we can use a double integral to optimize the efficiency of a production car's engine so it can use less fuel during operation.

Most modern cars use computers to run their engines. This computer, often called an ECU (engine control unit), controls the airflow into the engine, injection of fuel into the engine, and the ignition of the air-fuel mixture inside the combustion chamber.

The exact timing of igniting the air-fuel mixture is extremely critical to combustion efficiency. If ignited too early in an engine cycle, the air-fuel mixture won't be compressed enough to fully burn. If ignited too late, the air-fuel mixture won't have enough time to fully burn.

We can run tests on an engine and collect data for combustion efficiency being a function of engine RPM (revolutions per minute) and ignition timing. If we plot the data, we will see a two-variable function's surface plot like the one below:

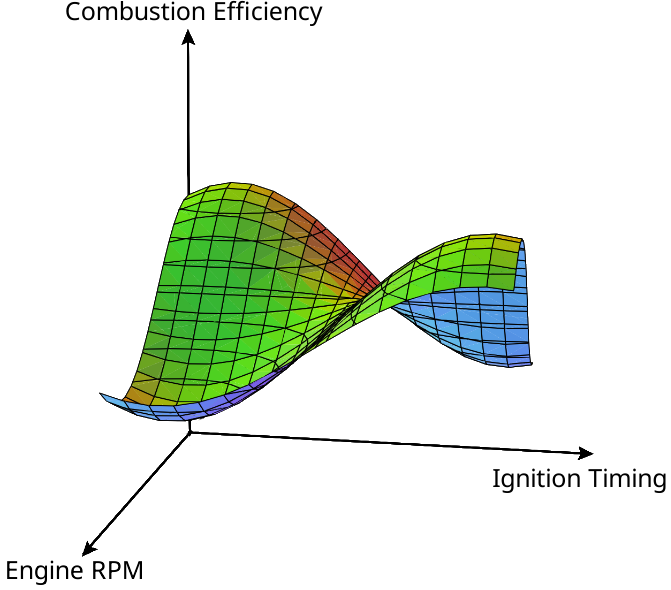
Since we have modeled the engine's efficiency as a function of two variables (engine RPM and ignition timing), we can easily calculate a double integral over a rectangular region on the engine RPM - ignition timing plane.

By calculating this double integral, we find the total volume between the surface and the engine RPM - ignition timing plane bound by the rectangular region we chose.

We can divide this volume by the area of our rectangular region. By doing so, we will end up with the average value of the combustion efficiency function over that rectangular region.

By knowing the average combustion efficiency of the engine over various engine operation parameters via our double integral, we can program the ECU to maximize power while minimizing fuel consumption!

Example Problem

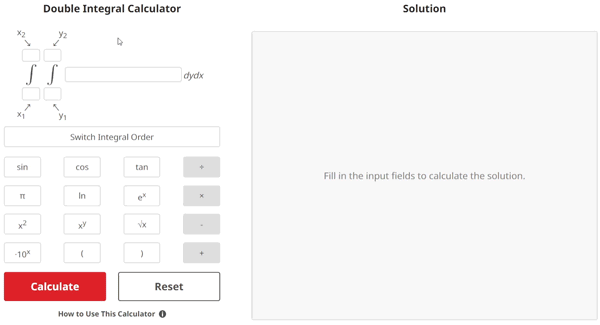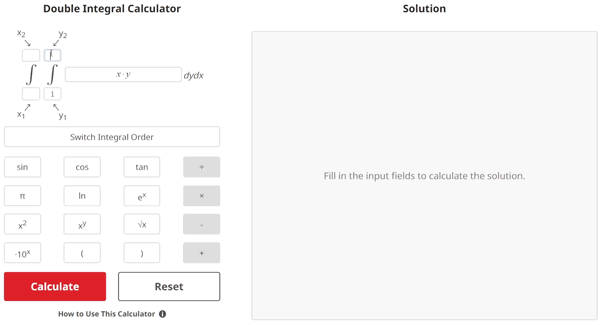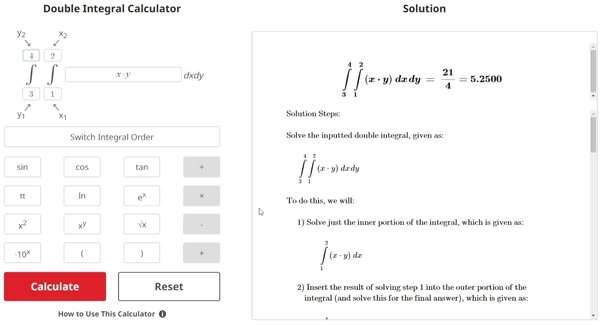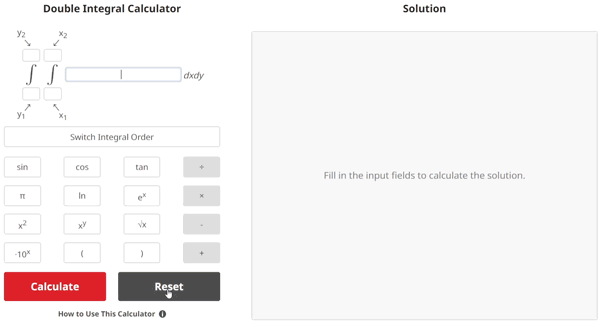
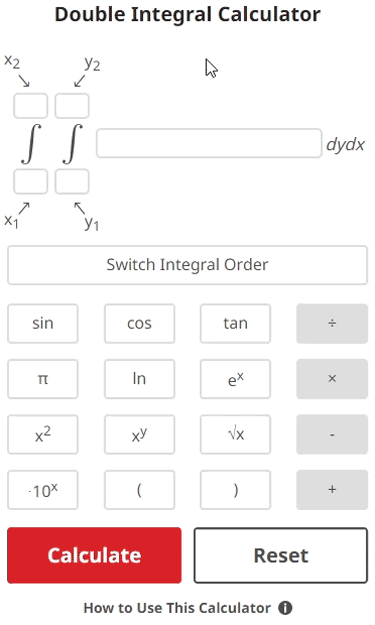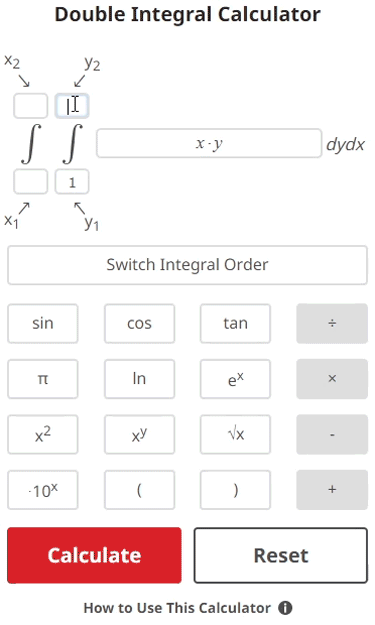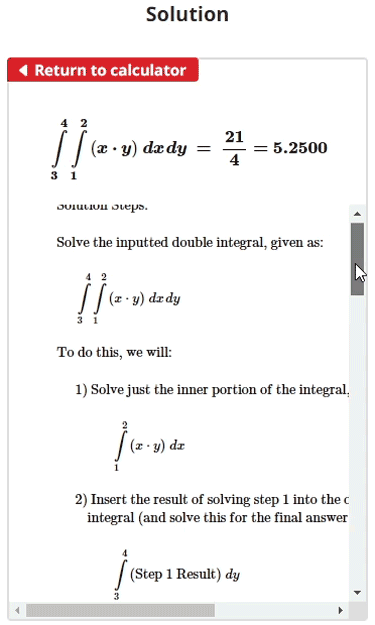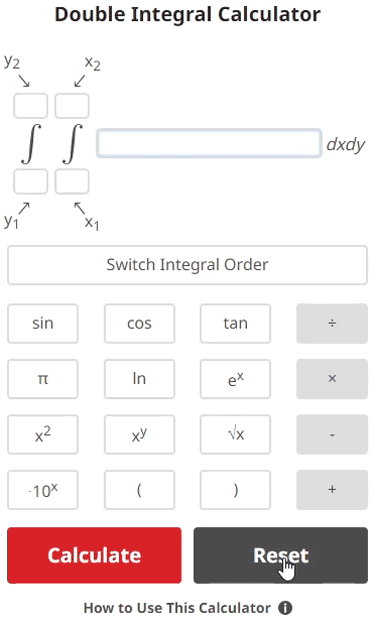
$$\begin{align}& \hspace{2ex} \text{Calculate the double integral given as:} \\ \\ & \hspace{5ex} \int \limits_{3}^{4} \int \limits_{1}^{2} \left(xy\right) \; dx\hspace{1pt} dy\\ \\ & \hspace{2ex} \text{To do this, we will:} \\ \\ & \hspace{5ex} \text{1) Solve just the inner portion of the integral, which is given as:} \\ \\ & \hspace{11ex} \int \limits_{1}^{2} \left(xy\right) \; dx\\ \\ & \hspace{5ex} \text{2) Insert the result of solving step 1 into the outer portion of the} \\ & \hspace{7ex} \text{integral (and solve this for the final answer), which is given as:} \\ \\ & \hspace{11ex} \int \limits_{3}^{4} \left( \text{Step 1 Result} \right) \; dy\\ \\ \\ & \hspace{2ex} \text{1) First, let's solve just the inner portion of the integral.}\\ \\ & \hspace{5ex} \text{1.1) Our full integral (with the inner portion shown inside the box)} \\ & \hspace{9ex} \text{is given as:} \\ \\ & \hspace{9ex} \int \limits_{3}^{4} \boxed{\int \limits_{1}^{2} \left(xy\right) \; dx}\hspace{1pt} dy\\ \\ & \hspace{9ex} \text{By removing the outer portion of the integral, we are left} \\ & \hspace{9ex} \text{with just the inner portion, which is given as:} \\ \\ & \hspace{12ex} \boxed{\int \limits_{1}^{2} \left(xy\right) \; dx}\\ \\ & \hspace{5ex} \text{1.2) Now we will take the antiderivative (also called an indefinite integral)} \\ & \hspace{9ex} \text{of this inner portion, but we will treat the variable }y\text{ as a constant } \\ & \hspace{9ex} \text{and take the antiderivative with respect to }x\text{. Doing so, we get:} \\ \\ & \hspace{9ex} \int_{}^{} \left(xy\right) \; dx\; = \; \boxed{\left(\frac{1}{2}\right) {x}^{2} y}\\ \\ & \hspace{5ex} \text{1.3) We can now finish evaluating this inner portion by plugging} \\ & \hspace{9ex} \text{in the limits of integration }x_{1} \text{ and }x_{2}\text{, and then simplifying} \\ & \hspace{9ex} \text{the resulting expression. Doing so, we get:} \\ \\ & \hspace{9ex} \left.\left(\frac{1}{2}\right) {x}^{2} y\: \right|_{1}^{2} \; = \;\left(\frac{1}{2}\right) {\left(2\right)}^{2} y - \left(\left(\frac{1}{2}\right) {\left(1\right)}^{2} y\right)\\ \\ & \hspace{12ex}\left(\frac{1}{2}\right) {\left(2\right)}^{2} y - \left(\left(\frac{1}{2}\right) {\left(1\right)}^{2} y\right)\; = \;2 y-\left(\frac{1}{2}\right) y\\ \\ & \hspace{15ex}2 y-\left(\frac{1}{2}\right) y\; = \; \boxed{\left(\frac{3}{2}\right) y}\\ \\ \\ & \hspace{2ex} \text{2) Now that we have solved the inner portion of the integral,} \\ & \hspace{4ex} \text{we can plug its result into the outer portion of the integral} \\ & \hspace{4ex} \text{and then solve that for the final answer.}\\ \\ & \hspace{5ex} \text{2.1) Our original, full integral (with the outer portion boxed)} \\ & \hspace{9ex} \text{is given as:} \\ \\ & \hspace{9ex} \boxed{\int \limits_{3}^{4}} \int \limits_{1}^{2} \left(xy\right) \; dx\hspace{1pt} \boxed{dy} \\ \\ & \hspace{9ex} \text{By removing the inner portion of the integral to isolate} \\ & \hspace{9ex} \text{the outer portion, and plugging in the evaluated} \\ & \hspace{9ex} \text{result of the inner portion, we end up with:} \\ \\ & \hspace{12ex} \boxed{\int \limits_{3}^{4} \left(\left(\frac{3}{2}\right) y\right) \; dy}\\ \\ & \hspace{5ex} \text{2.2) Now we will take the antiderivative (also called an indefinite} \\ & \hspace{9ex} \text{integral) of this outer portion. Doing so, we get:} \\ \\ & \hspace{9ex} \int_{}^{} \left(\left(\frac{3}{2}\right) y\right) \; dy\; = \; \boxed{\left(\frac{3}{4}\right) {y}^{2}}\\ \\ & \hspace{5ex} \text{2.3) We can now finish solving for the final answer by plugging} \\ & \hspace{9ex} \text{in the limits of integration }y_{1} \text{ and }y_{2}\text{, and then simplifying} \\ & \hspace{9ex} \text{the resulting expression. Doing so, we get:} \\ \\ & \hspace{9ex} \left.\left(\frac{3}{4}\right) {y}^{2}\: \right|_{3}^{4} \; = \;\left(\frac{3}{4}\right) {\left(4\right)}^{2} - \left(\left(\frac{3}{4}\right) {\left(3\right)}^{2}\right)\\ \\ & \hspace{12ex}\left(\frac{3}{4}\right) {\left(4\right)}^{2} - \left(\left(\frac{3}{4}\right) {\left(3\right)}^{2}\right)\; = \;12-\frac{27}{4}\\ \\ & \hspace{15ex}12-\frac{27}{4}\; = \; \boxed{\frac{21}{4} = 5.2500} \\ \\ & \hspace{9ex} \boxed{\boxed{ \int \limits_{3}^{4} \int \limits_{1}^{2} \left(xy\right) \; dx\hspace{1pt} dy\; = \;\frac{21}{4} = 5.2500}}\end{align}$$

How the Calculator Works

The Double Integral Calculator is coded in HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

The HTML constructs the calculator's architecture. The calculator's frame, buttons, text, and other entities are all defined by the HTML code.

The CSS provides the graphical element of the calculator. The specific colors, shapes, and animations of the calculator's components are created and defined with the CSS code.

JS is what makes the calculator tick. When we click any of the buttons, the JS code handles the response to that click. Also, the mathematic procedure and solution steps creation are all performed by the JS code.