Related Content
Laplace Transform Calculator

To get unlimited answers, .
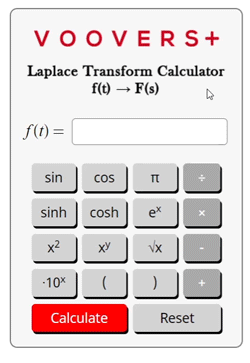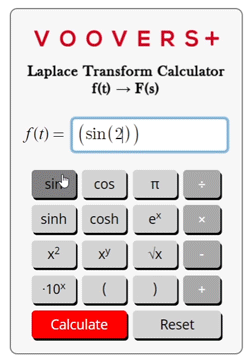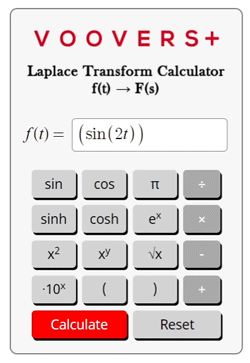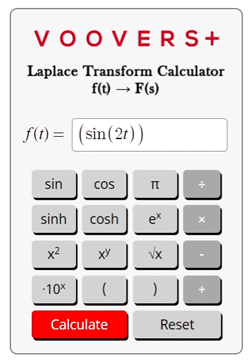
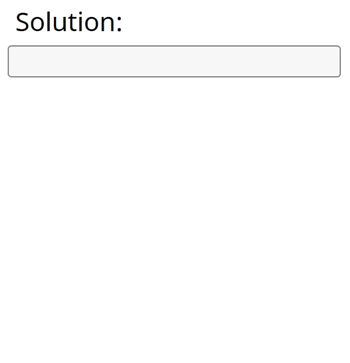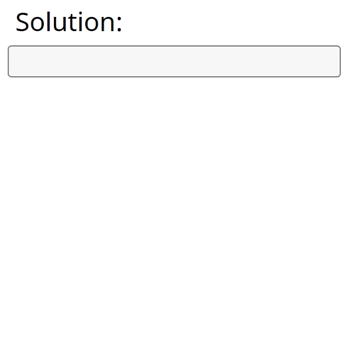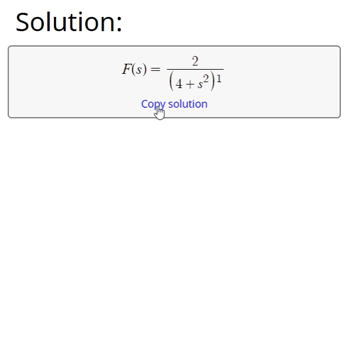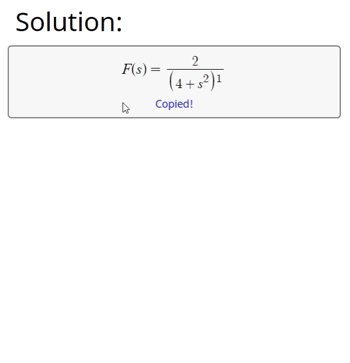
Trying to calculate an inverse Laplace transform instead? Try our inverse Laplace transform calculator.
Laplace Transform Lesson
Lesson Contents
What is a Laplace Transform?
By using the above Laplace transform calculator, we convert a function f(t) from the time domain, to a function F(s) of the complex variable s.
The Laplace transform provides us with a complex function of a complex variable. This may not have significant meaning to us at face value, but Laplace transforms are extremely useful in mathematics, engineering, and science.
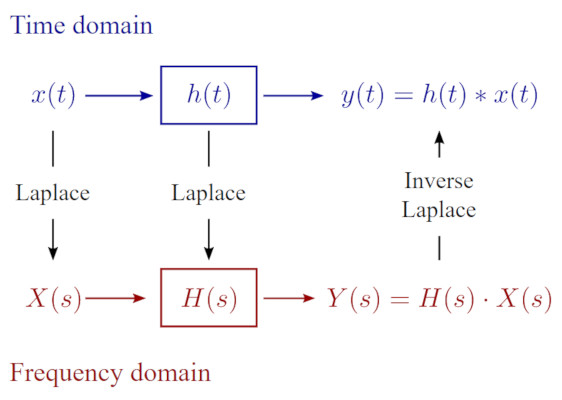
The Laplace transform is capable of transforming a linear differential equation into an algebraic equation. Linear differential equations are extremely prevalent in real-world applications and often arise from problems in electrical engineering, control systems, and physics. Having a computer solve them via Laplace transform is very powerful and useful.
It is important that we know what we intend by saying “Laplace transform calculator.” There is such thing as a bilateral Laplace transform, which combines the normal Laplace transform with the inverse Laplace transform. The inverse Laplace transform is when we go from a function F(s) to a function f(t). It is the opposite of the normal Laplace transform.
The calculator above performs a normal Laplace transform. Only calculating the normal Laplace transform is a process also known as a unilateral Laplace transform. This is because we use one side of the Laplace transform (the normal side), and neglect to use the inverse Laplace transform side.
How to Calculate a Laplace Transform by Hand
To perform the Laplace transform of an elementary function we usually consult the Laplace transform table. This table can be memorized but doing so is not necessary unless the table is restricted from use on a quiz or exam.


