Inverse Laplace Transform Calculator

F(s) =

Solution:

Help

Trying to calculate a Laplace transform instead? Try our Laplace transform calculator.

Inverse Laplace Transform Lesson

What is an Inverse Laplace Transform?

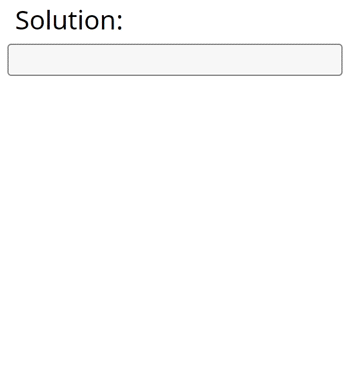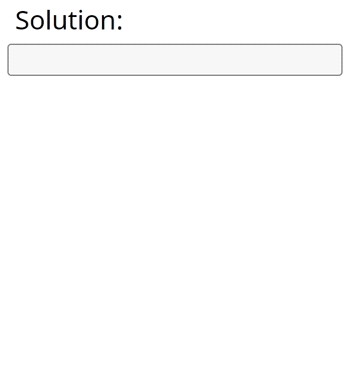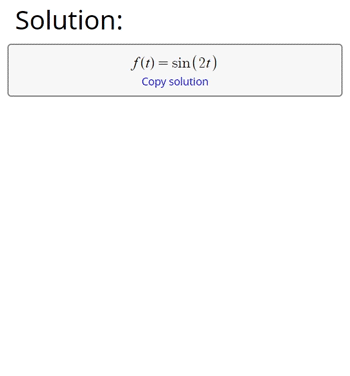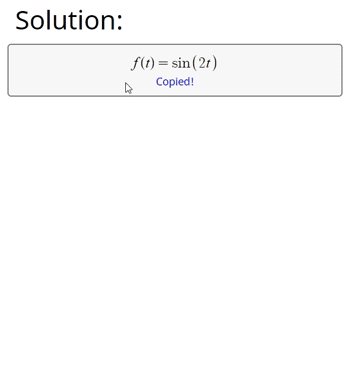
By using the inverse Laplace transform calculator above, we convert a function F(s) of the complex variable s, to a function f(t) of the time domain. To understand the inverse Laplace transform more in-depth, let’s first check our understanding of the normal Laplace transform.

The Laplace transform converts f(t) in the time domain to F(s) which provides us with a complex function of a complex variable. The inverse Laplace transform is exactly as named — the inverse of a normal Laplace transform.

An inverse Laplace transform can only be performed on a function F(s) such that L{f(t)} = F(s) exists. Because of this, calculating the inverse Laplace transform can be used to check one’s work after calculating a normal Laplace transform.

Although it is still useful, the inverse transform is not often used as a standalone tool for math and science applications. It is generally used to complement the normal transform.

How to Calculate an Inverse Laplace Transform by Hand

To perform a normal or inverse Laplace transform of an elementary function, we may consult the table of transforms below. It is worthwhile to have a basic working knowledge of this table, but memorizing it should not be necessary as it is usually provided during quizzes/tests, or can be referenced when applicable.

If calculating an inverse transform, simply find your function or subfunction on the right column under F(s). Follow its row to the left, and the corresponding function in the f(t) column is the inverse Laplace transform of your F(s).

How the Calculator Works

The inverse Laplace transform calculator on this page is written entirely in JavaScript (JS) and powered by a computer algebra system (CAS). This allows it to run in your device’s internet browser JS engine, providing nearly instantaneous answers at the click of a button.

Your inputted function F(s) is fed to the CAS, where the bulk of the calculations occur. The CAS treats the function as a set of symbols, preserving each character exactly as inputted and with no roundoff error or truncation error. Essentially, it performs similar steps to a human with a paper and pencil.

Once the inverse transform is finalized, it is formatted and converted to LaTeX (a math rendering language). The LaTeX code is then rendered in the answer area of the calculator. If there is no solution or an error occurs, an error notice will instead be displayed.