Integral Calculator

f(x) =

x_lower = x_upper =

Help

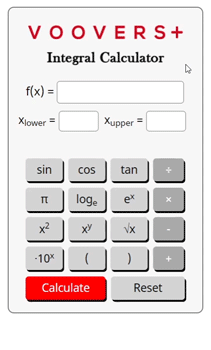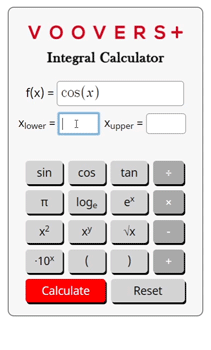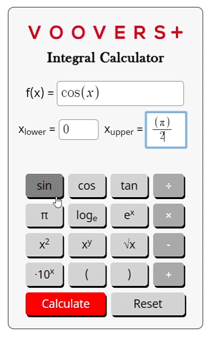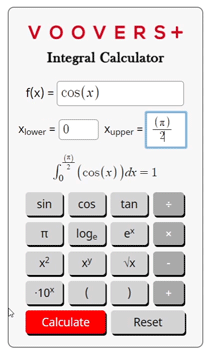
Trying to calculate the indefinite integral or antiderivative of your function? Try our antiderivative calculator.

Lesson on Integrals

What is an Integral?

An integral transforms a function in way that can describe area, volume, or other properties. Integrals are the inverse of derivatives.

There are two main types of integrals: definite and indefinite. A definite integral uses a closed interval (also called the limits of integration) to calculate a scalar value such as area under the curve or volume under a surface.

An indefinite integral is simply an antiderivative (the inverse of a derivative) in that it transforms the function but does not calculate a scalar value.

Hand Calculating an Integral

The first step of calculating a definite and indefinite integral of a function is the same. We take the antiderivative of the function. If performing an indefinite integral, we are done after taking the antiderivative, just make sure not to forget the constant of integration C.

If performing a definite integral, we must then apply the fundamental theorem of calculus. If we are calculating the integral of f(x) on the interval [a, b] and F(x) is the antiderivative of f(x), the fundamental theorem of calculus tells us the solution is F(b) – F(a).

How the Calculator Works

The calculator on this page uses a computer algebra system (CAS) to symbolically compute your definite integral. It preserves the function and limits of integration as “symbols” which reduces computer round-off error and allows a more accurate solution.

When you click the “compute solution” button, the inputted function and limits are processed by code that filters the inputs and parses the function into math operations that can be recognized by the CAS. Then, the antiderivative of the function is taken by the CAS before it applies the fundamental theorem of calculus to get the solution.

That scalar solution is sent back to this page and rendered by the word processing language called LaTeX, which is what allows the integral notation to be formatted in a way that is easy to read.