What is an Antiderivative?

The above calculator finds the antiderivative of the function you provided with respect to the variable chosen. An antiderivative is used in the process of calculating an integral. It is exactly as its name implies: the opposite of a derivative.

The derivative of an antiderivative of a function is the original function. Here’s an example of an antiderivative versus a derivative:

$$\begin{align} & \text{Antiderivative: } \int \left( x^{2} \right) dx \; \longrightarrow \; \frac{1}{3}x^{3} \\ \\ & \text{Derivative: } \; \frac{d}{dx} \frac{1}{3} x^{3} \; \longrightarrow \; x^{2} \end{align}$$

As we can see from the results of these two operations, by taking the derivative of our antiderivative takes us right back to the original function. As stated earlier, we take the antiderivative when doing definite and indefinite integrals. Antiderivatives and integrals tell us how much area is under the curve for a function's graph.

Generally, when performing an integral we will refer to an operation as an antiderivative when we are more focused on the actual math operations rather than what the integral will result in. For example, when we calculate a definite integral, we will take the antiderivative of the function, and then apply the fundamental theorem of calculus to get the actual integral result.

How to Calculate an Antiderivative by Hand

The way we calculate an antiderivative or indefinite integral depends on the expression. For many common expressions, we can apply what are known as “integral rules” which are essentially shortcuts for calculating the antiderivative. The integral rules are applied to expressions similarly to how derivative rules are applied.

In the case of an expression that does not have an integral rule, other methods that take longer and are sometimes more tedious can be employed. Expressions that are too complex for using the power rule can be integrated by parts. An example of an antiderivative that requires integration by parts is the integral of ln(x).

When we are faced with a composite function, such as a trig function of a polynomial, u-substitution is very useful (u-substitution can be considered a reversal of the chain rule used when calculating derivatives).

Antiderivative Example Problem

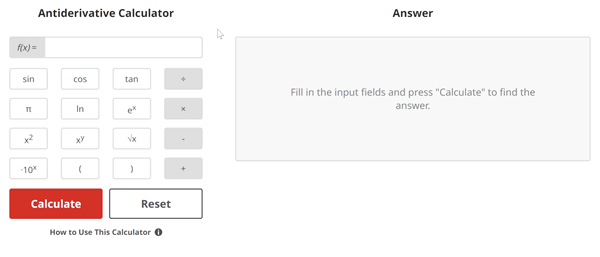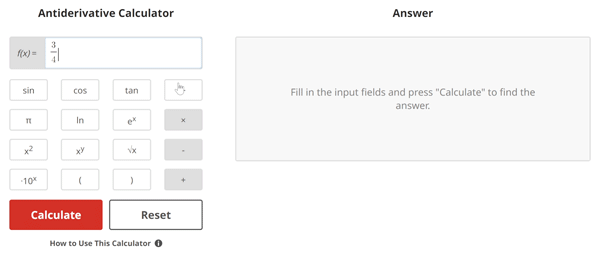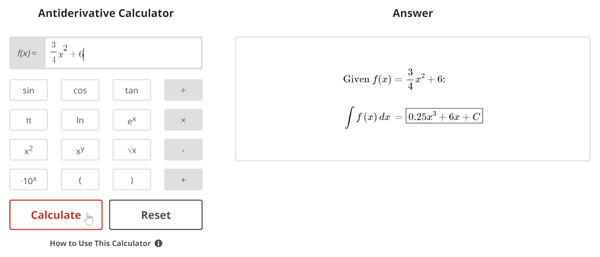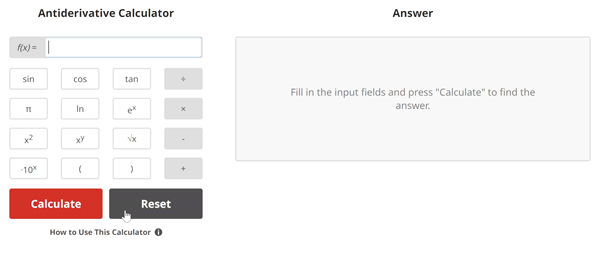
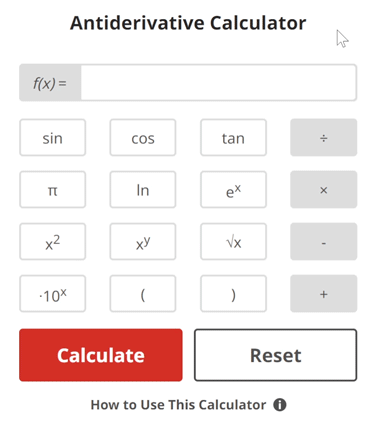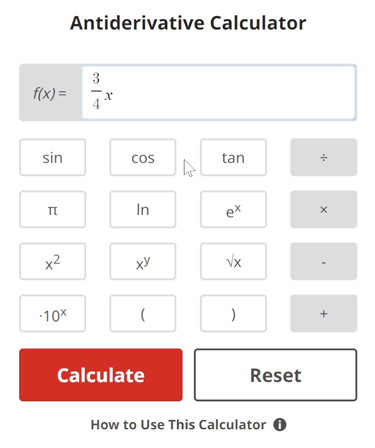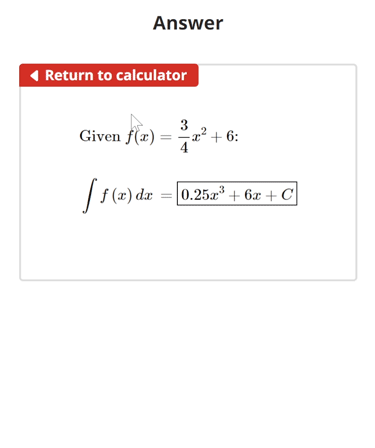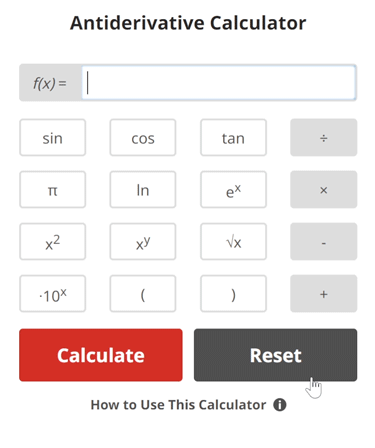
Find the antiderivative with respect to x of the function f(x) = ³⁄₄x² + 6.

Solution:

1. We will use the reverse power rule to take the antiderivative of this function.
2. Applying the reverse power rule gives us ³⁄_{4(2 + 1)}x^{(2 + 1)} + 6x + C.
3. Simplifying this gives us ¹⁄₄x³ + 6x + C.
4. The antiderivative with respect to x of ³⁄₄x² + 6 is ¹⁄₄x³ + 6x + C.

How the Calculator Works

The Antiderivative Calculator is made up of HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

HTML serves as the basic framework of the calculator. Specifically, HTML is used to define the various entities such as the calculator input field and answer field so that we can assign visual and functional properties.

CSS is used to style the calculator itself. Everything from the color of the "Calculate" button, to the size of the answer field is controlled with CSS.

JS is used to perform the actual calculations based on the user's input and provides a smooth and adaptive experience across different electronic devices.