System of Equations Solver

Number of equations:

Equation 1:

Equation 2:

Help

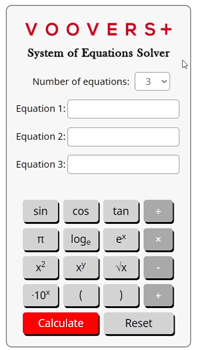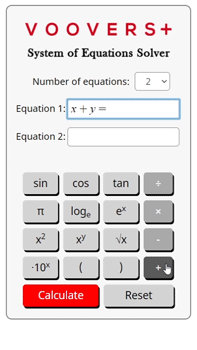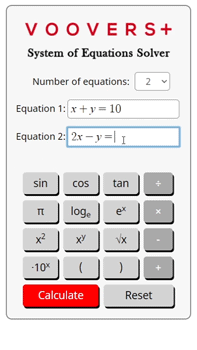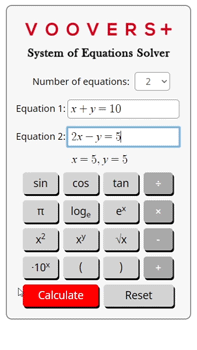
Lesson on Systems of Equations

Rules for Solving Systems of Equations

When solving a linear or nonlinear system of equations, we want to have a determined system where the number of equations is equal to the number of variables.

If there are fewer equations than variables, the system is underdetermined and may have zero or any number of solutions. If there are more equations than variables, the system is overdetermined and may have zero or any number of solutions.

A linear system of equations may have zero, one, or infinite solutions. A nonlinear system of equations may have zero or any number of solutions. There are zero solutions if the equations are parallel but never intersect. There are infinite solutions if the equations are identical and lay on top of each other over the entire domain.

How to Solve a System

There are many techniques available for solving a system of equations, however, they all leverage basic algebra, and any system of equations can be solved by isolating a variable, substituting it into another equation, isolating the next variable, and so forth.

Let’s solve a linear two-equation system using isolation and substitution. The system we will solve is:
Equation 1: 2x + y = 8
Equation 2: x – y = 4

Solution:
1.) Let’s isolate x in the second equation. Moving y to the right side of the equation results in x = y + 4.
2.) We may now substitute that value of x into the first equation. By doing so, we get 2(y + 4) + y = 8. Simplifying it results in 3y + 8 = 8.
3.) Solving that equation for y, we get y = 0.
4.) We may substitute y’s solution into either equation. Substituting it into the first equation, we get 2x + 0 = 8. Solving for x, we get x = 4.
5.) The solution to the system of equations is x = 4, y = 0.

How the Calculator Works

The Voovers System of Equations Solver is written in the programming language JavaScript (JS) and uses a JS native computer algebra system (CAS). Your device’s internet browser has a built-in JS engine, which allows the calculator to run locally and provide instant solutions.

When the calculate button is pressed, your equations are fed into a JS array that stores each equation in its own entry. Then, the array is fed to the CAS which performs the calculations that find the solution. For nonlinear systems, it returns the first solution that satisfies the equations.

After calculations are finished, the solution is converted to LaTeX (a math rendering language) and displayed in the answer area of the calculator. Sometimes there is no solution, infinite solutions, or an error during calculations. When these anomalies occur, an error message is displayed instead of an answer.