The Four Kinematic Equations

• Equation 1:     v = v₀ + at
• Equation 2:     v² = v₀² + 2a(Δx)
• Equation 3:     x = x₀ + v₀t
• Equation 4:     x = x₀ + v₀t + ¹/₂at²

Kinematic Variables

• x - Displacement
• v - Velocity
• a - Acceleration
• t - Time

These are the four variables at play with the kinematic equations. The equations describe the motion of an object that is subject to constant acceleration. By leveraging the equations, we can solve for the initial and final values of these variables.

Important: Directionality of the Variables

Displacement, velocity, and acceleration are all directional, whereas time is non-directional. Directional variables will have a positive value when their vector points in the positive direction, and a negative value when their vector points in the negative direction. Since time is non-directional, it will always have a positive value.

When using the kinematic equations to solve problems, it is helpful to choose a direction for positive x, v, and a. Sometimes this direction is given in the problem statement. The opposite of the positive direction will be the negative direction.

When to use the Kinematic Equations

Kinematics is the study of object motion without reference to the forces that cause motion. The kinematic equations are simplifications of object motion. Three of the equations assume constant acceleration (equations 1, 2, and 4), and the other equation assumes zero acceleration and constant velocity (equation 3).

When an object motion problem falls into these categories, we may use the kinematic equations to solve it. For example, we can use them to figure out how far a projectile flies as long as the projectile experiences constant acceleration during its flight. Another example of a simple and effective use of the kinematic equations is when a car driving at constant velocity. Since it has zero acceleration, we may use the equation that has no acceleration terms (equation 3).

How to Choose a Kinematic Equation

We must decide which kinematic equation is best for what we are solving. Generally, kinematics problems involve solving for some unknown. The unknown could be initial displacement, final displacement, change in displacement, initial velocity, final velocity, acceleration, or time.

We choose an equation based on what is known and what is not known. In some cases, we must use several equations sequentially to find the value of our unknown. The example problems below give more insight for the process of choosing an equation.

Kinematic Equations Example Problems

Kinematic Equation 1 Example

A projectile is fired from the chamber of a cannon and accelerates at 1500 m/s² for 0.75 seconds before leaving the barrel. What is the projectile’s velocity as it leaves the barrel of the cannon?

Solution:

1. Since the projectile is not moving before it is fired, our initial velocity will be zero. We are given the values of acceleration (1500 m/s²) and time (0.75 seconds), so the equation we will use is v = v₀ + at.
2. Since we know the values of all variables except final velocity, we may plug in our known values to find v, this gives us v = (0 m/s) + (1500 m/s²)(0.75 seconds) = 1125 m/s.
3. The projectile's velocity is 1125 m/s as it leaves the barrel.

Kinematic Equation 2 Example

A sprinter is moving at 5 m/s when they reach 20 meters into their race. They maintain a constant acceleration of 2 m/s² through 40 meters into the race. What is the sprinter’s velocity 40 meters into the race?

Solution:

1. We know the values of initial velocity (5 m/s), acceleration (2 m/s²), and change in displacement (40 – 20 = 20 meters). The equation we will use is v² = v₀² + 2a(Δx).
2. Since we know the values of all variables except final velocity, we may plug in our known values and find v.
   v² = (5 m/s)² + 2(2 m/s²)(20 meters)
   v² = 105
   v = 10.25 m/s
3. The sprinter's velocity is 10.25 m/s at 40 meters into the race.

Kinematic Equation 3 Example

A car is 200 meters away from a building and starts driving away from the building at 20 m/s. How far away is the car from the building after driving for 6 seconds?

Solution:

1. We know the values of initial displacement (200 meters), initial velocity (20 m/s), and time in motion (6 seconds). We must find final displacement. The kinematic equation we will use is x = x₀ + v₀t.
2. Since we know the values of all variables but one, we may plug in our known values to find the unknown value of x.
   x = (200 meters) + (20 m/s)(6 seconds) = 320 meters
3. After driving for 6 seconds, the car is 320 meters away from the building.

Kinematic Equation 4 Example

A person is standing 6 meters behind you. They throw a ball over your head with a horizontal velocity of 20 m/s. The ball experiences a constant 4 m/s² of horizontal deceleration while in flight and takes 2 seconds to land. How far in front of you does the ball land?

Solution:

1. We know the values of initial displacement (-6 meters), initial velocity (20 m/s), acceleration (-4 m/s²), and time (2 seconds). The equation we will use is x = x₀ + v₀t + ¹/₂at².
2. Since we know the values of all variables except final displacement, we may plug in our known values and find x.
   x = (-6 meters) + (20 m/s)(2 seconds) + ¹/₂(-4 m/s²)(2 seconds)²
   x = -6 + 40 - 8
   x = 26 meters
3. The ball lands 26 meters in front of you.

Bonus Kinematics Lesson

What is Projectile Motion?

Earlier we mentioned that projectile motion problems can be solved by using the kinematic equations. While projectile motion is just one of the many types of problems we come across in kinematics, it is very useful to understand exactly what it is.

By definition, projectile motion is the motion of an object or particle that is only affected by the force of gravity. A projectile follows a parabolic trajectory similar to when a ball is thrown. This parabolic trajectory is also called a ballistic trajectory.

How to Solve Projectile Motion

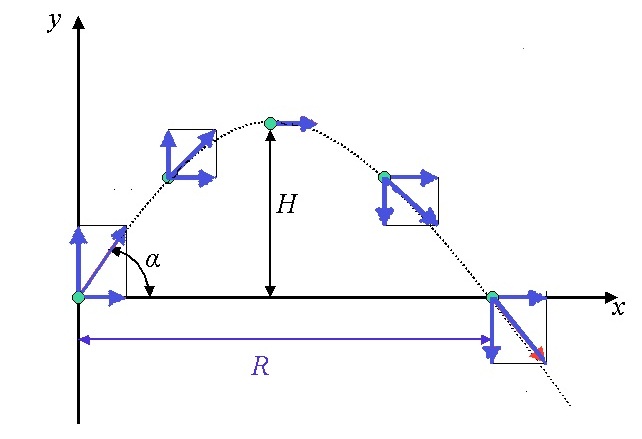
Since we neglect the force of air resistance in projectile motion, we can figure out how far a projectile will fly by decomposing its velocity into vertical and horizontal components. The horizontal component of velocity will be constant during the flight. The vertical component of velocity will affect the projectile's time of flight, or hang time.

Here's the equations for a projectile's horizontal and vertical motion. They are derived from the kinematic equations.

• a_x = 0
• v_x = v₀cos(α)
• x = v₀cos(α)t + x₀
• a_y = -g
• v_y = v₀sin(α)
• t = ^2v_y/_g

Projectile Motion Example

A ball is thrown from the surface of Earth at 25 m/s on an angle of 30° above the horizontal. Neglecting air resistance, how far does the ball travel horizontally before hitting the ground?

Solution:

1. First, let's set our known variables.
   v₀ = 25 m/s
   α = 30°
   g = 9.81 m/s².
2. Let's find the velocity components.
   v_x = v₀cos(α) = 25cos(30°) = 21.65 m/s
   v_y = v₀sin(α) = 25sin(30°) = 12.5 m/s
3. Now we can find the hang time, and use the hang time to calculate horizontal distance traveled.
   t = ^2v_y/_g = ^2(12.5)/_9.81 = 2.55
   x = v₀cos(α)t + x₀ = 25cos(30°)(2.55) + 0 = (21.65)(2.55) = 55.21
4. The ball travels horizontally for 55.21 meters before hitting the ground.