Related Content
Programmers and Teachers:
Nikkolas K.
Tutor and degreed Aerospace Engineer
Determinant Calculator
Size:
A =
You have one free use of this calculator.
Get unlimited calculations here.
You have one free use of this calculator.
Determinant Lesson
Lesson Contents
What is a Determinant?
The determinant of a matrix is a number that can be calculated from a square matrix. It can be used for solving systems of linear equations and tells us about certain properties of the matrix, such as the volume scaling factor of the linear transformation described by the matrix.
The matrix determinant can also help tell us if the matrix has an inverse or not. You can use this calculator to check if the matrix’s determinant is not zero. If it is not zero, it has an inverse matrix and you can use the inverse matrix calculator to find it. If the determinant is zero, there is no inverse of the matrix.
Also, the determinant helps us find the eigenvalues. This is because it leads us to the characteristic polynomial of the matrix. The characteristic polynomial is used in solving for eigenvalues.
How to Calculate a Determinant by Hand
Hand calculating the determinant of a matrix varies based on the size of the matrix. For a 1×1 matrix, the determinant is the number inside the matrix. For anything 2×2 and larger, we use shortcut methods that have a special order of multiplying, adding, and subtracting components.
The shortcut methods consist of explicit multiplication, addition, and subtraction of matrix entries in a very specific order. Below is an image of the method for a 3×3 matrix. For an in-depth explanation of how to hand calculate the determinant, see our determinant of a matrix lesson.
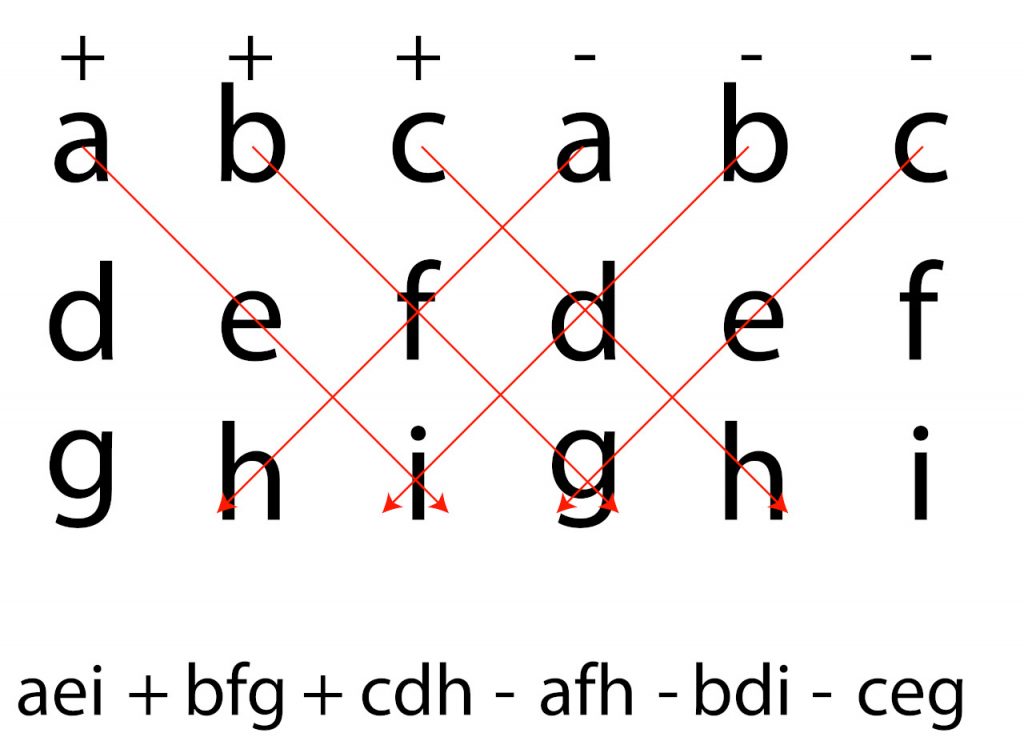
Example of a shortcut method for the determinant of a 3×3 matrix.
How the Calculator Works
The Voovers Determinant Calculator is written in JavaScript (JS), which is a programming language supported by your internet browser’s built-in JS engine. JS code runs locally and within the browser, allowing for instant calculations.
The meat and potatoes of the code is a JS native computer algebra system (CAS) that uses similar analytical methods to what is shown in the image above. Your inputted matrix is sent to the CAS where the determinant is calculated. The final answer is then converted to LaTeX code which allows the math expressions to render on the webpage.
The CAS treats calculations symbolically which preserves numbers as their exact value. If the CAS used numerical methods, it would store each matrix entry as a floating-point number with roundoff error, which would result in a less accurate solution. By using symbolic methods, an exact solution is made possible.
Sometimes an error occurs during calculations or the inputted matrix entries do not allow for a solution to be found. When these anomalies occur, an error message is displayed in the answer area.