Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Determinant of a Matrix
Lesson Contents
What is the Matrix Determinant?
The determinant is a number we can calculate from a square matrix. It describes certain properties of the matrix and can be used for solving linear systems of equations. The determinant of a matrix is notated with vertical bars similar to absolute value notation. For example, the determinant of a matrix A is notated as |A|.
The method for finding the determinant depends on the size of the matrix. In this lesson, we will show how to find the determinant of 1×1, 2×2, and 3×3 matrices. A 4×4 or larger matrix takes very long to calculate by hand and is very tedious. For matrices of that size, we recommend using a calculator such as the Determinant Calculator.
How to Find the Determinant of a 1x1 Matrix
The determinant of a 1×1 matrix is the number inside the matrix.
For example, if matrix A = [5] then the determinant is |A| = 5.
How to Find the Determinant of a 2x2 Matrix
For a 2×2 matrix, if matrix A = 
then the determinant is |A| = ad – bc.
An easy way to remember the order of components that get multiplied and subtracted is to imagine the diagonal line and direction that the components are on.
The 2×2 determinant goes top left to bottom right minus top right to bottom left. That order of diagonal and direction gives us ad – bc.
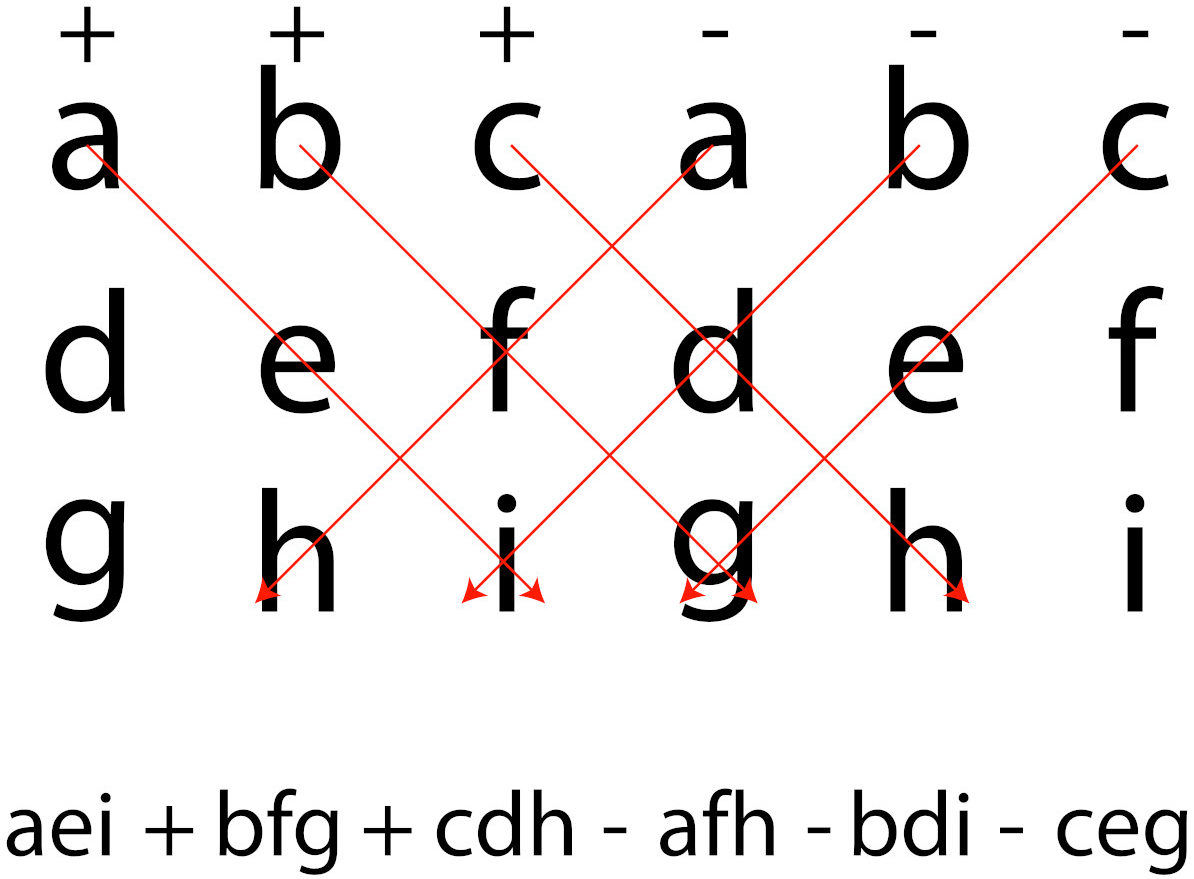
How to Find the Determinant of a 3x3 Matrix
If matrix A = 
then the determinant |A| = 
.
The top row components of the 3×3 matrix are always the leading coefficients on each smaller 2×2 determinant within the formula. Make sure to remember that there is a negative sign in front of b!
A simple way to remember the 3×3 matrix determinant is to imagine it as three 2×2 matrix determinants. The top row components are leading coefficients in front of each 2×2 determinant.
Break the 3×3 matrix down into the top row 1×3 matrix, and the bottom two rows as a 2×3 matrix. The 2×3 matrix has three combinations of 2×2 matrices in it. Simply memorize the pattern of 1×3 components that multiply by the three 2×2 matrix determinants.
