Maclaurin Series Calculator

f(x) =

Series order: n =

Solution:

Help

Maclaurin Series Lesson

Why do we use a Maclaurin Series?

A Maclaurin series is a special subset of the Taylor series. A Taylor series provides us a polynomial approximation of a function centered on the point a, whereas a Maclaurin series is always centered on a = 0. Because the behavior of polynomials can be easier to understand than functions such as sin(x), we can use a Maclaurin series to help in solving differential equations, infinite sums, and advanced physics problems. In fact, if we make a Maclaurin series of infinite terms, it will represent the function perfectly.

However, a finite Maclaurin series is just an approximation of the function, where the accuracy in which the series represents the function is positively correlated with the number of terms in the series. Carrying out more terms of a Maclaurin series will give us a more accurate representation of the function.

The number of terms in the series is directly linked to the degree of the Maclaurin series. The degree is the maximum n value written in the sigma notation of the formula given below. The number of terms in the series is n + 1 since the first term is created with n = 0. The highest power in the polynomial is n = n.

How to Calculate a Maclaurin Series

The formula for calculating a Maclaurin series for a function is given as:

Where n is the order, and f⁽ⁿ⁾(0) is the nth order derivative of f(x) as evaluated at x = 0. The series will be most accurate near the centering point. As we move away from the centering point a = 0, the series becomes less accurate of an approximation of the function.

As we can see, a Maclaurin series may be infinitely long if we choose, but we may also choose to make our series as many or few terms/accurate as we want. We can set a maximum n value to make it an n order series.

How the Calculator Works

This calculator is written in the programming language JavaScript (JS) and utilizes a JS-native computer algebra system (CAS). When you click the calculate button, the entire script is run by your device’s internet browser JS engine, allowing for near-instant results.

The CAS employs symbolic computation to create the Maclaurin series expansion. It treats every character as a symbol, rather than a number value. In practice, this avoids computer roundoff error and provides the user with a perfectly accurate analytical solution, being in the form of a mathematical expression.

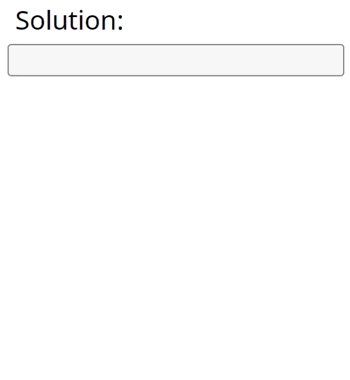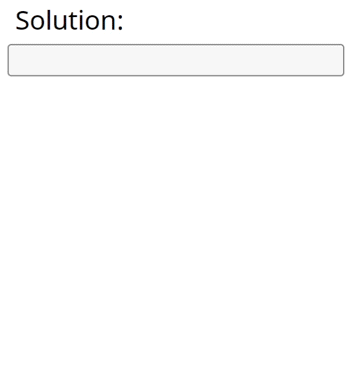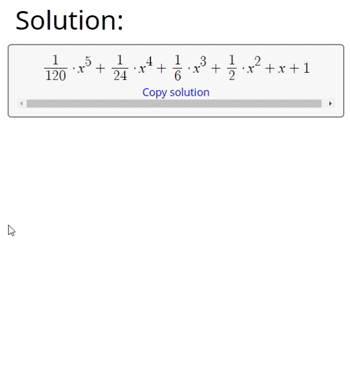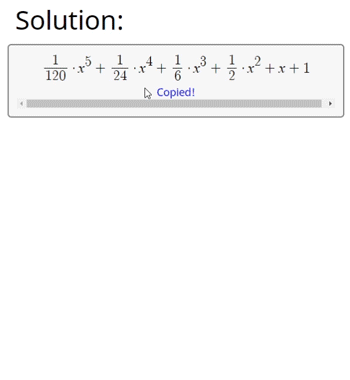
When the solution is fully calculated, it is converted to LaTeX code. LaTeX is a math markup and rendering language that allows us to graphically display math equations and expressions on a webpage. That final LaTeX solution code is rendered on the page in the answer area.