Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Limit Calculator
f(x) =
Limit as x →
You have one free use of this calculator.
Click here for unlimited calculations.
You have one free use of this calculator.
Lesson on Limits
Lesson Contents
What is a Limit?
Sometimes a function f(x) will be undefined at certain x values. Since the function is not defined at those locations, it can be hard to determine the function’s behavior. For example, f(x) = 1⁄x is undefined at x = 0 since 1⁄0 is undefined.
However, we can take the limit of f(x) at x = 0. Taking the limit of a function helps to describe its behavior around a point. The limit is defined as the value that a function f(x) approaches as x approaches the point a. Limit notation is given as:
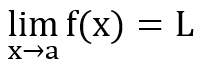
Where L is the limit of f(x) as x approaches a. This notation describes a two-sided limit, where x approaches a from both sides. We can take a left-hand or right-hand limit where x approaches from one side by adding a minus sign (for left-hand limit, ex: x → a–) or a plus sign (for a right-hand limit, ex: x → a+) next to the a.
How to Hand Calculate a Limit
To take the limit of a function, we plug in numbers very close to the x value we are approaching. Plugging in incrementally closer numbers gives us an idea of what the function would be if it were not undefined at that point.
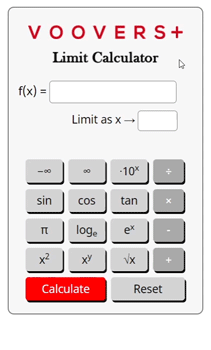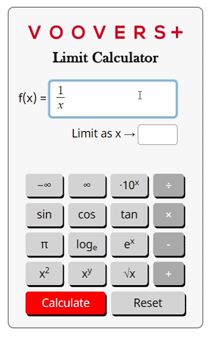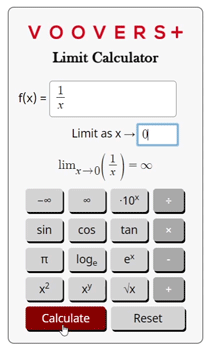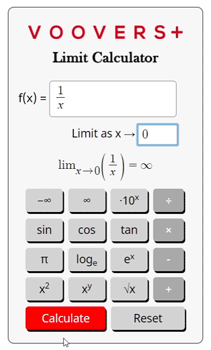
As an example, let’s find the left-hand limit of f(x) = 1⁄x as x approaches 0. Since x → 0–, we will start by plugging in numbers that are barely under 0.
1.) f(-0.1) = 1⁄-0.1 = -10
2.) f(-0.001) = 1⁄-0.001 = -1000
3.) We can see that approaching 0 from the left side causes the function to become a larger negative value. The function’s value is approaching negative infinity. Therefore, the limit is -∞.
How the Calculator Works
The calculator on this page uses a computer algebra system (CAS) to symbolically compute your limit. The computer algebra system follows the same algebra and calculus rules that we use when calculating by hand with a paper and pencil.
Since the software treats the function and numbers as symbols, it can calculate a perfectly accurate solution in some cases because it avoids computer round-off error. The symbolic nature of it also means it can calculate limits that approach oo and -oo.
Once the limit is computed, its value is sent back to this page. The answer is formatted in limit notation with the markup language LaTeX which is then rendered from text into the image that you actually see.
