Rectangular to Polar Calculator

Help

Rectangular and Polar Coordinates Lesson

Rectangular Coordinates vs. Polar Coordinates

Notated as (x, y), rectangular coordinates (also called Cartesian coordinates) give us the position of a point in terms of its location relative to the x-axis and y-axis. Notated as (r, θ), polar coordinates give us the position of a point with radius measured as a distance away from the origin and angle measured counter-clockwise off the positive x-axis (also called the polar-axis or r-axis).

Imagine the polar coordinate angle θ is measured on a clock. 0° is 3 o’clock, 90° is 12 o’clock, 180° is 9 o’clock, and 360° is back to 3 o’clock. If the angle is negative, go clockwise. For example, -90° is at the 6 o’clock position.

Both styles of coordinates have their strengths and weaknesses and are best used in different situations. Rectangular coordinates are very easy to use for polynomial functions that use x and y as variables. For functions that use r and θ as variables, polar coordinates are easier to work with.

How to Hand Calculate the Conversion

The formulas for converting rectangular to polar are given as:

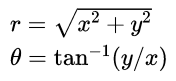
Pay very close attention to the units used when evaluating tan^-1(y/x) to find θ. If using a calculator, make sure the output unit on the calculator matches the unit written next to the answer. If we calculate in radians but write degrees as the unit next to our angle it is incorrect.

Example Problem

Convert the rectangular coordinates (3, 6) to polar coordinates. Express the polar angle in degrees.

Solution:
1.) First, let’s find our radius coordinate. Applying the formula gives us:
r = (3² + 6²) = 6.708
2.) Now let’s find the angle coordinate. Applying the formula gives us:
θ = tan^-1(6/3) = 63.435°
3.) Our point in polar coordinates is (r, θ) = (6.708, 63.435°).

How the Calculator Works

The calculator on this page is written in the languages HTML, CSS, PHP, and Python. HTML and CSS form the interface that you interact with. The PHP component receives your inputted numbers and feeds them to the Python script, which calculates the coordinate conversion.

Inside the Python script, your input the x and y coordinates are plugged into the radius and angle equations that are shown above. The outputted radius and angle are then both rounded to the fourth decimal place.

The rounded numbers are then sent back here and displayed in the answer area. This all happens very quickly because a computer processor is doing the work. However, as humans, we can easily hand calculate the conversion with paper and pencil algebra and a scientific calculator just as accurately!