Related Content
Eigenvector Calculator

To get unlimited answers, .
Eigenvector Lesson
Lesson Contents
What is an Eigenvector?
Eigenvectors are a set of vectors associated with a system of linear equations/matrix. The combination of the eigenvalues and eigenvalues of a system of equations/matrix is very useful in various mathematics, physics, and engineering problems.
“Eigen” is German for “own”. These semantics describe the relationship between the eigenvalues and eigenvectors; each eigenvalue has a corresponding eigenvector, and vice versa. The eigenvalues and eigenvectors of any linear system of equations/matrix can be found if the matrix is square. A square matrix is one that has an equal number of columns and rows. Non-square matrices will have complex/imaginary eigenvalues and eigenvectors.
How to Hand Calculate Eigenvectors
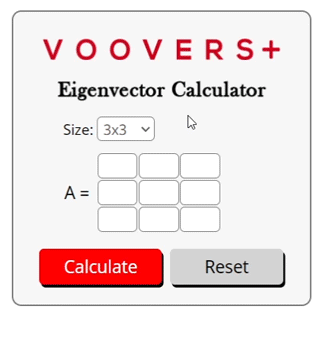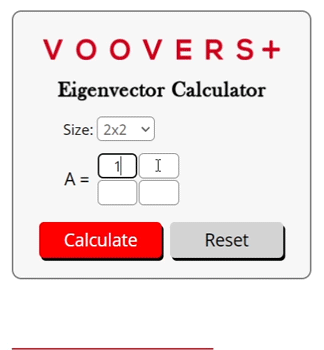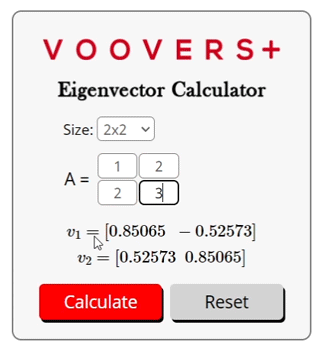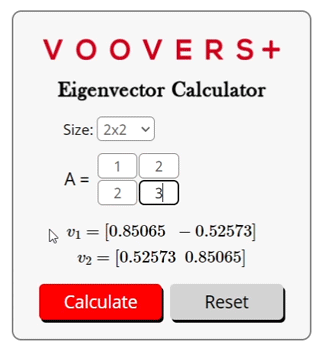
The basic representation of the relationship between an eigenvector and its corresponding eigenvalue is given as Av = λv, where A is a matrix of m rows and m columns, λ is a scalar, and v is a vector of m columns. In this relation, true values of v are the eigenvectors, and true values of λ are the eigenvalues.
For the value of a variable to be true, it must satisfy the equation such that the left and right sides of the equation are equal. Since we will solve for the eigenvalues first, the eigenvectors will satisfy the equation for each given eigenvalue. There may be more eigenvectors than eigenvalues, so each value of λ may have multiple values of v that satisfy the equation. It is possible for there to be an infinite number of eigenvectors for an eigenvalue, but usually there will only be a few distinct eigenvectors.
The equation Av = λv can be rearranged to A – I = 0 where I is the identity matrix. Then, we can proceed to carrying out the matrix multiplication and subtraction operations which will result in a polynomial. This polynomial is set equal to zero. Then, the roots of the terms can be solved for. The roots of these terms are the eigenvalues. When the eigenvalues are known, we can plug them into the equation Av = λv and find out eigenvectors.
In a matrix of m columns and rows, there can be as few as zero eigenvalues, and as many as m eigenvalues. As stated earlier, each of these eigenvalues could have any number of eigenvectors associated with it. This means that we can expect the number of eigenvectors of a system to be anywhere from zero to infinity. Now, that’s not a particularly small range of values, but we can expect the number of eigenvectors to be less than twenty when working with standard 3×3 and 4×4 matrices.
How the Calculator Works
This calculator is written in JavaScript (JS) and uses a JS native computer algebra system (CAS) for computations. Your inputted matrix is converted to a 2-dimensional JS array and then fed to the CAS.
The CAS then uses a numerical routine called the “Jacobi method” to find the eigenvectors and eigenvalues. This numerical routine involves stepping through approximated calculations that are repeated very many times until convergence to an accurate solution is reached. It then returns the eigenvalues and eigenvectors. The eigenvectors are built into an output array that is formatted into LaTeX (a math rendering language) and displayed in the answer area.
Because computer processors are so much more capable of fast, simple calculations than a human, the calculator can go through these routines in the blink of an eye and return you a result that is accurate to a minimum of the fifth decimal place.
This calculator finds the eigenvectors and eigenvalues simultaneously but displaying both can get messy for large systems/matrices. If you would like to see the eigenvalues of your matrix, visit our eigenvalue calculator. Between the two calculators, the order of eigenvalues will match the order of eigenvectors.


