What is a Special Right Triangle?

There are certain right triangles with dimensions that make remembering the side lengths and angles very easy. These are known as special right triangles. Special right triangles fall into two categories: angle-based and side-based. We will go over the common and useful angle-based and side-based triangles in this lesson.

Angle-Based Special Right Triangles

The common angle-based special right triangles are:

• 45-45-90 Triangle
• 30-60-90 Triangle

The triangle name describes the three internal angles. These triangles also have side length relationships that can be easily memorized. The image below shows all angle and side length relationships for the 45-45-90 and 30-60-90 triangles.

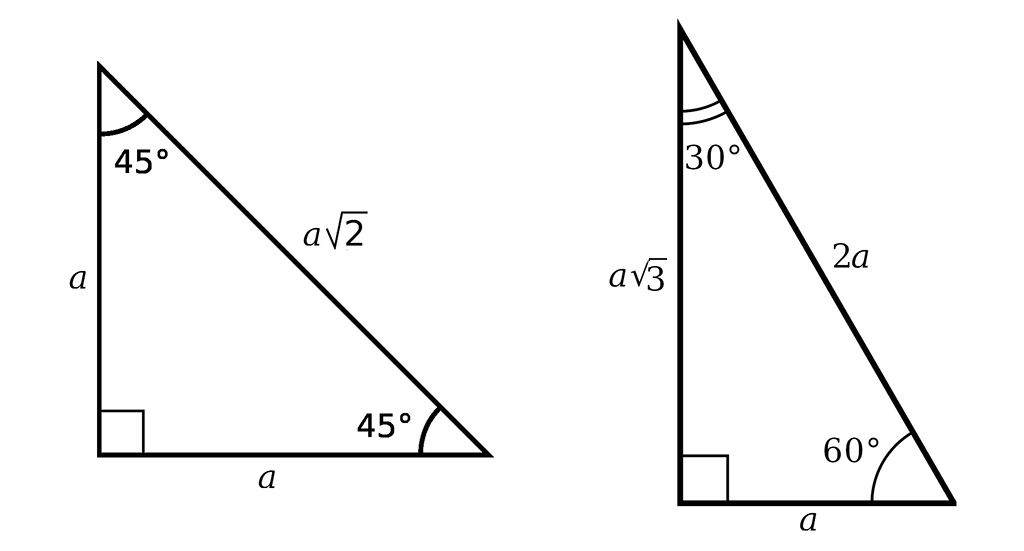
Side-Based Special Right Triangles

The common side-based special right triangles are:

• 3-4-5 Triangle
• 5-12-13 Triangle

The triangle name describes the ratio of side lengths. For example, a 3-4-5 triangle could have side lengths of 6-8-10 since they have a 3-4-5 ratio. The image below shows all side length and angle relationships for the 3-4-5 and 5-12-13 triangles.

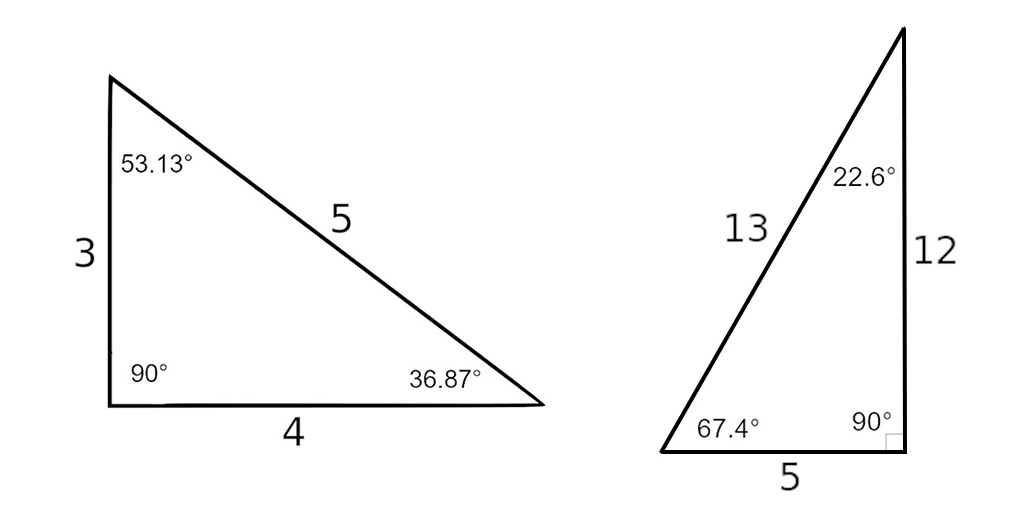
How to Solve Special Right Triangles

The reason for memorizing the special right triangles is that it allows us to quickly determine a missing side length or angle. The first step in solving any special right triangle problem is to identify what type of triangle it is.

Once the type of special right triangle has been identified, we are usually able to determine the missing side length or angle. Take a look at the practice problems below to see how we do this.

Special Right Triangle Practice Problems

Problem 1

A 45-45-90 triangle has two sides with a length of 10. What is the 3rd side length?

Solution:

The 45-45-90 triangle relationship tells us that the hypotenuse is square root of 2 times the leg. Since the leg is 10, the hypotenuse (3rd side length) is 10√2.

Problem 2

A triangle has side two internal angles of 30° and 90°, and two side lengths of 5 and 5√3. What is the 3rd side length?

Solution:

This must be a 30-60-90 triangle because of the two given angles. The 30-60-90 relationship tells us that the side lengths are a, 2a, and a√3. We can see from the two given sides that a = 5 and we are missing the 2a side. So, the 3rd side length is 2 · 5 = 10.

Problem 3

A triangle has side lengths of 20 and 48. What is the 3rd side length?

Solution:

Let's figure out which side-based special right triangle this is. First, reduce the side lengths by a common denominator. ²⁰⁄₄ = 5 and ⁴⁸⁄₄ = 12, so this must be a 5-12-13 triangle. 13 · 4 = 52, so the 3rd side length is 52.

Problem 4

A triangle has side lengths of 21 and 28. What is the 3rd side length?

Solution:

Let's figure out which side-based special right triangle this is. First, reduce the side lengths by a common denominator. ²¹⁄₇ = 3 and ²⁸⁄₇ = 4, so this must be a 3-4-5 triangle. 5 · 7 = 35, so the 3rd side length is 35.