What is a 45 45 90 Triangle?

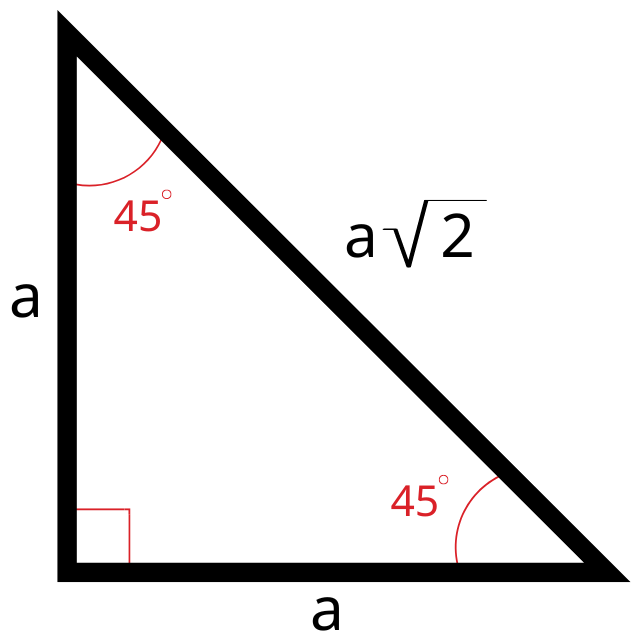
A 45 45 90 triangle is a special right triangle with angles of 45, 45, and 90 degrees. It is also considered an isosceles triangle since it has two congruent sides.

We memorize the 45 45 90 pattern so we can quickly recognize if a right triangle has two congruent legs and two 45 degree internal angles. When we recognize these properties, we can quickly find the value of side lengths and internal angles.

In summary, we should recognize a right triangle as 45 45 90 if we notice one or both of the following conditions:

• The two legs are congruent.
• It has one or two internal angles of 45 degrees.

45 45 90 Pythagorean Theorem Shortcut

Since the two legs of a 45 45 triangle are congruent, we can simplify the Pythagorean theorem. Remember that the Pythagorean theorem tells us a² + b² = c².

Since a = b, c² = 2a². We can choose either leg to be notated as a since it is equal to b. This gives us the hypotenuse length equation as:

c = √(2a²), c = a√2

This means we can simply multiply one of the legs by the square root of 2 to get our hypotenuse length!

45 45 90 Triangle Rules

Four handy rules that apply to the 45 45 90 triangle:

1. The three internal angles are 45, 45, and 90 degrees.
2. The legs are congruent.
3. The hypotenuse length is √2 times the leg length.
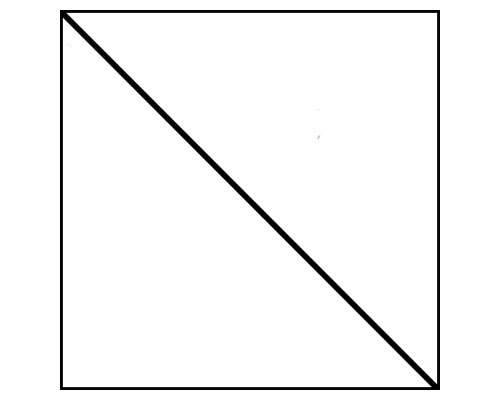
4. It can be created by cutting a square in half at the diagonal as shown below.

Finding the Area and Perimeter

The equation for area of a 45 45 90 triangle is given as:

A = ¹/₂b²

Where A is the area and b is the leg length.

The equation for perimeter of a 45 45 90 triangle is given as:

P = 2b + c

Where P is the perimeter, b is the leg length, and c is the hypotenuse length.

If we only have the length of the leg, we can use the following equation:

P = 2b + b√2

45 45 90 Triangle Example Problems

Example Problem 1

Two sides of a 45 45 90 triangle have a length of 10. What is the 3rd side length?

Solution:

The 3rd side is the hypotenuse. To find the hypotenuse, we will use rule #3. Multiplying the leg length 10 by √2 gives us a hypotenuse length of 10√2 = 14.142.

Example Problem 2

Two of the sides of a 45 45 90 triangle have a length of 25 and 25√2. What is the length of the 3rd side?

Solution:

We were given two sides of the triangle, and they are not congruent. This means they cannot be the legs. A right triangle's leg will always be shorter than its hypotenuse, so we know that the 25 side is a leg of this triangle. The legs of a 45 45 90 triangle are congruent, so the length of the 3rd side is 25.

Example Problem 3

The leg length of a 45 45 90 triangle is 5. What is the hypotenuse length?

Solution:

Using rule #3, c = a√2. Plugging in our leg length of 5 in place of a, we get a hypotenuse length of 5√2 = 7.071.

Example Problem 4

The hypotenuse length for a 45 45 90 triangle is 20√2. What are the leg lengths?

Solution:

We will again use rule #3 to solve this. We know that c = b√2, so a = 20. The leg lengths are 20.

Example Problem 5

Which of the following triangles are 45 45 90 right triangles?

• Triangle 1: 3, 4, 5
• Triangle 2: 5, 12, 13
• Triangle 3: 5, 20, 25
• Triangle 4: 3, 6, 8
• Triangle 5: 4, 4, 4√2

Solution:

Triangle 5 is the only 45 45 90 triangle in the list.