The 30 60 90 Triangle Theorem

A 30-60-90 triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees. Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified.

Imagine cutting an equilateral triangle vertically, right down the middle. Each half has now become a 30 60 90 triangle. This visualization is very useful for remembering that the hypotenuse is twice as long as the short leg on a 30 60 90 triangle.

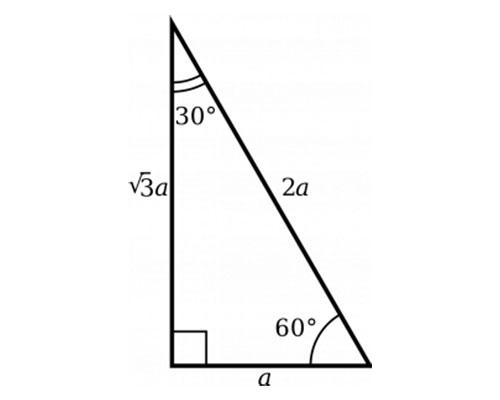
30 60 90 Triangle Rules

To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90. To solve for the side lengths, a minimum of 1 side length must already be known.

If we know that we are working with a right triangle, we know that one of the angles is 90 degrees. If we find that another angle is either 30 or 60 degrees, it is confirmed to be a 30 60 90 triangle. This is because the internal angles of a triangle will always sum to 180 degrees.

Once we know the angles follow the 30 60 90 ratio, we can apply the relation that the hypotenuse is twice as long as the short leg.

The side opposite to the 30 degree angle is the shortest, the side opposite to 60 degree angle is the second shortest (or second longest), and the side opposite to the 90 degree angle is the hypotenuse and the longest.

A Proof of why a 30 60 90 Triangle Works

Let’s take a look at the Pythagorean theorem being applied to a 30 60 90 triangle. Remember that the Pythagorean theorem is a² + b² = c². Using a short leg length of 1, long leg length of 2, and hypotenuse length of √3, the Pythagorean theorem is applied and gives us:

1² + (√3)² = 2², 4 = 4

The theorem holds true with the side lengths of a 30 60 90 triangle.

30 60 90 Triangle Example Problem

Let's work through an example problem together to reinforce our understanding of 30 60 90 triangles.

If the short leg of a 30 60 90 triangle is 5 meters long, what are the two other side lengths in meters?

Solution:

1. We know from the image and ratio that the other two side lengths are √3a and 2a.
2. Since a = 5, let's substitute 5 in for a.
3. The two other side lengths are 5√3 and 10 meters long.