What is a 3 4 5 Triangle?

A 3 4 5 triangle is an SSS right triangle (meaning we know the three side lengths). If we know two of the side lengths and they are congruent with the 3 4 5 ratio, we can easily determine the third side length by using the ratio. The other common SSS special right triangle is the 5 12 13 triangle.

We call it the 3 4 5 "ratio" because the side lengths do not need to be exactly 3, 4, and 5, but rather can be any common factor of these numbers. For example, a right triangle with side lengths of 6, 8, and 10 is considered a 3 4 5 triangle. Its side lengths are a common factor of 2 of the 3 4 5 ratio.

A 3 4 5 triangle is classified as a scalene triangle since all three sides lengths and internal angles are different.

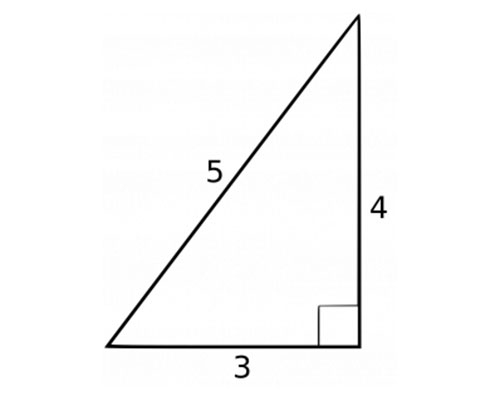
List of 3 4 5 Triangles

The following are some of the most common sets of 3 4 5 triangle side lengths. We do not need to memorize this list as long as we are aware that the ratio can be multiplied by a common factor to produce any of these sets of side lengths.

• -3 4 5
• -6 8 10
• -9 12 15
• -12 16 20
• -15 20 25

3 4 5 Triangle Angles

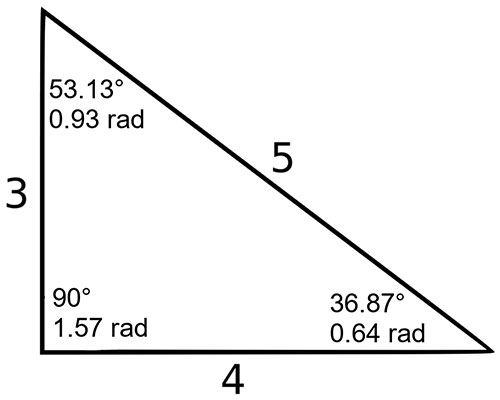
The three internal angles in degrees are 36.87, 53.13, and 90. The three angles in radians are 0.64, 0.93, and 1.57. See the image below for the location of these angles.

How to Construct a 3 4 5 Triangle

We can construct a 3 4 5 triangle by starting with a two lines that meet at a right angle. Make the vertical line about 3/4 as long as the horizontal line. Then, connect the ends of these two lines with a straight line.

The connecting line makes our hypotenuse, which will end up being about 5/4 as long as the horizontal side, and about 5/3 as long as the vertical side. Label the short leg 3, the long leg 4, and the hypotenuse 5.

Equations for Area and Perimeter

The equation for area of a 3 4 5 triangle is given as:

Area = ¹/₂bh

This becomes area = ¹/₂(3)(4) = 6 when it is a true 3 4 5 triangle. If the triangle is scaled from the ratio by a common factor, we can multiply 6 by that common factor to get the area.

The equation for perimeter is given as:

Perimeter = a + b + c = 3 + 4 + 5 = 12 for a true 3 4 5 triangle.

If the triangle is scaled from the ratio by a common factor, we can multiply 12 by that common factor to get the perimeter.

Proof of the 3 4 5 Triangle

Let’s take a look at the math that proves the existence of the 3 4 5 ratio. We are going to use the standard side lengths of 3 and 4 to look for the 3rd side length using the Pythagorean theorem.

1. Remember that a² + b² = c².
2. 3² + 4² = 9 + 16 = 25
3. 5² = 25, so the 3 4 5 right triangle ratio is satisfied.

Let’s prove it again with a different example. We are going to multiply the numbers of the ratio by a common factor of 2.

1. 6² + 8² = 36 + 64 = 100
2. 10² = 100, so the 3 4 5 right triangle ratio is satisfied.
3. This proves the ratio holds true even when scaled by a common factor.

3 4 5 Triangle Example Problem

Which of the following triangles are 3 4 5 right triangles?

• Triangle 1: 8, 8, 25
• Triangle 2: 9, 12, 15
• Triangle 3: 23, 27, 31
• Triangle 4: 12, 16, 20
• Triangle 5: 6, 8, 10

Solution:

1. Triangle 2 is the 3 4 5 ratio multiplied by a common factor of 3.
2. Triangle 4 is the 3 4 5 ratio multiplied by a common factor of 4.
3. Triangle 5 is the 3 4 5 ratio multiplied by a common factor of 2.
4. Therefore, triangles 2, 4, and 5 are 3 4 5 right triangles.