5 12 13 Triangle Lesson
What is a 5 12 13 Triangle?
The 5 12 13 triangle is an SSS special right triangle with the ratio between its side lengths as 5, 12, and 13. It is a common Pythagorean triple that is worth memorizing to save time when dealing with right triangles. The other common SSS special right triangle is the 3 4 5 triangle.

Using the 5 12 13 Ratio to our Advantage
A 5 12 13 triangle is considered a scalene triangle because all three of its sides have different lengths. If we come across a right triangle and two of the known sides are part of the 5 12 13 ratio, we can immediately determine that the third side will be the remaining number in the ratio. Note that the "13" side will always be the hypotenuse. The 5 12 13 ratio is scalable and applies to any right triangle with sides that are any common multiple of the numbers 5, 12, and 13.
List of 5 12 13 Triangles
The following triangle side lengths are common multiples of the 5 12 13 ratio and are all considered 5 12 13 triangles. It is not necessary to memorize this list, but it is very useful to understand that 5 12 13 is a ratio that may manifest itself as smaller or larger numbers than the ratio itself.
- 2.5 6 6.5
- 5 12 13
- 7.5 18 19.5
- 15 36 39
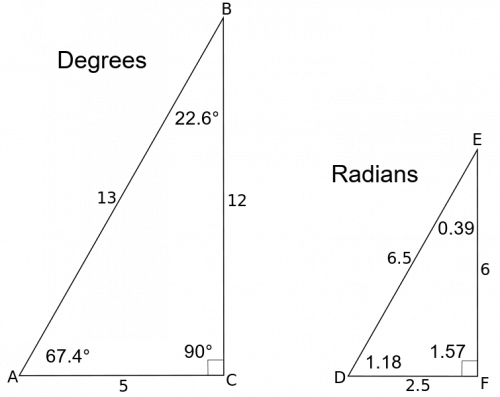
5 12 13 Triangle Angles
A 5 12 13 triangle contains the following internal angles in degrees:
- 22.6°, 67.4°, 90°
And in radians:
- 0.39, 1.18, and 1.57
It is not expected to memorize these. We can use the soh cah toa rule and inverse trigonometric functions to solve for the angles since we know the side lengths. See the image below for a visual of these angles.
What is the Area of a 5 12 13 Triangle?
Calculating the area of a 5 12 13 triangle, we get A = (1⁄2)(5)(12) = 30. If the triangle conforms to the 5 12 13 ratio but is scaled, i.e. a 2.5 6 6.5 triangle, we still use the two shorter sides as the base and height. In this case, the area would be (1⁄2)(2.5)(6) = 7.5.
5 12 13 Triangle Example Problem 1
Find the third side length of the 5 12 13 right triangle that has side lengths of 39 and 15.
Solution:
- Since we know this is a 5 12 13 triangle scaled from the ratio by an unknown factor, we must determine which two sides are given.
39/15 = 2.6
12/5 = 2.5
13/5 = 2.6 - Therefore, we have been given the "13" and "5" sides. We will now multiply by a ratio to get the "12" side.
- (12⁄13)(39) = 36
- The third side length is 36.
5 12 13 Triangle Example Problem 2
Which of the following sets of side lengths constitute a 5 12 13 triangle?
- Triangle 1: 4, 9, 11.5
- Triangle 2: 10, 24, 26
- Triangle 3: 6, 13, 14
- Triangle 4: 20, 48, 52
Solution:
The side lengths of triangles 2 and 4 constitute a 5 12 13 triangle.

