What is Sohcahtoa?

Sohcahtoa is a word that helps us remember how to use sine, cosine, and tangent. Here's what sohcahtoa means:

• Soh — Sine of angle is Opposite over Hypotenuse.
• Cah — Cosine of angle is Adjacent over Hypotenuse.
• Toa — Tangent of angle is Opposite over Adjacent.

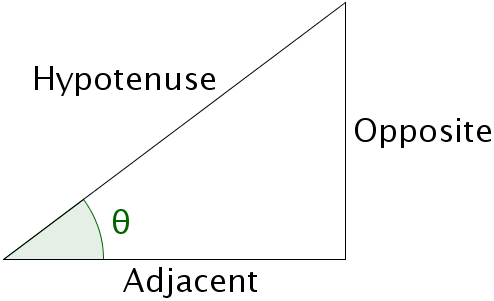
We can use sohcahtoa to create three different equations for finding the value of angle θ in the right triangle like shown below. They are given as:

• sin(θ) = ^opposite/_hypotenuse
• cos(θ) = ^adjacent/_hypotenuse
• tan(θ) = ^opposite/_adjacent

When to use Sohcahtoa

Sohcahtoa is applicable to any situation that involves a right triangle. Since we use right triangles to solve all kinds of problems in math, science, and engineering, knowing how to use sohcahtoa is extremely important!

How to use Sohcahtoa

A right triangle is made up of two shorter sides, called legs, and one longer, diagonal side, called the hypotenuse. The leg that touches the angle being measured is called the adjacent side. The other leg, which doesn't touch the angle, is called the opposite side.

We can find any of the three angles inside of a right triangle if the two of the three side lengths are known. Sohcahtoa gives us three different options for which two sides to use when calculating the angle.

Sohcahtoa Example Problem

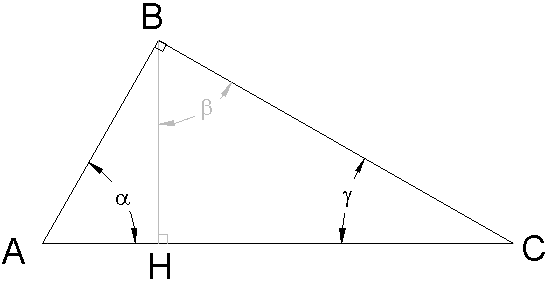
In the image below, side BC is 6 meters long, and the height H is 3 meters. What is the value of angle β in degrees?

Solution:

1. Even though the main outer triangle is not a right triangle, there is a right triangle formed by the height line and the two sides to its right. Therefore, we can use sohcahtoa to solve.
2. We have two lengths: the hypotenuse and the adjacent side.
3. Cah tells us that the cosine of an angle is equal to the adjacent over hypotenuse.
   cos(β) = ^adj/_hyp = ³/₆
   β = cos^-1(³/₆)
   β = 60°
4. The angle β = 60°.