Related Content
Arc Length Calculator

To get unlimited answers, .
Arc Length Lesson
Lesson Contents
What is Arc Length?
Arc length is the distance traveled from one point to another point along a curve. Since an arc can be defined by the curve of a function, there are an infinite number of possible arc shapes.
This calculator and lesson focus on the circular arc which is a section of a circle. Generally, we define a circular arc by its radius and angle. A circular arc can be any fraction of a complete circle. For example, a circular arc of radius 5 and angle 36° is 1⁄10 or 10% of a circle of radius 5.
Hand Calculating the Arc Length
To hand calculate the length of a circular arc, we use the basic arc length formula. The formula is given as:
s = rθ
Where s is the arc length, r is the radius of the arc, and θ is the angle in radians. To see how the formula is used, let’s go through an example together.
Example problem:
A circular arc has an angle of 3 radians and a radius of 12. What is the length of the arc?
1.) We can plug the given values directly into the formula s = rθ.
2.) s = (12)(3)
3.) s = 36
4.) The length of the arc is 36.
How the Calculator Works
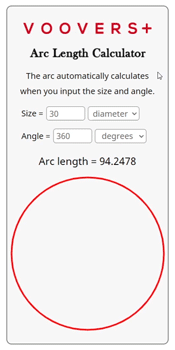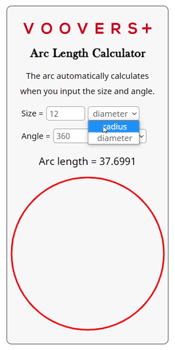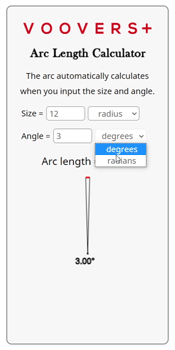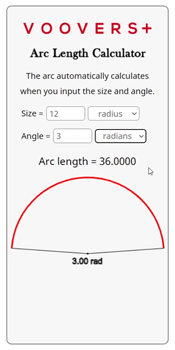
The calculator on this page is written in the programming language JavaScript. The JavaScript code runs in your internet browser when an input change is detected. Therefore, the arc length and arc drawing automatically update.
The code itself uses the same basic arc length formula that is given above. The size and angle units are detected, and values converted to radius and radians if needed. Then, the size and angle are plugged into the equation. The answer is rounded to the nearest 4th decimal place and displayed as the arc length.
The arc is drawn at a scale of 296 pixels wide so that it can fit within the width of a phone screen. The angle indication lines use sine and cosine relations to connect the ends of the arc to the center point. Other than some basic code, the calculator only uses basic geometry and trigonometry equations to calculate and draw your arc length!


