Normal Distribution Lesson
What is the Normal Distribution?
In statistics, the normal distribution is a type of continuous probability distribution that tells us values near the mean are most likely to occur. If you hear someone say "bell curve" they are referring to the normal distribution. It is commonly called a bell curve because it is shaped like a bell.
Normal distributions are extremely important in statistics because they describe many real-world, naturally occurring data sets. In a normal distribution, the curve is centered on the mean and extends out several standard deviations in either direction. The "bell curve" shape of a normal distribution is defined by the empirical rule (see our empirical rule lesson for full explanation).
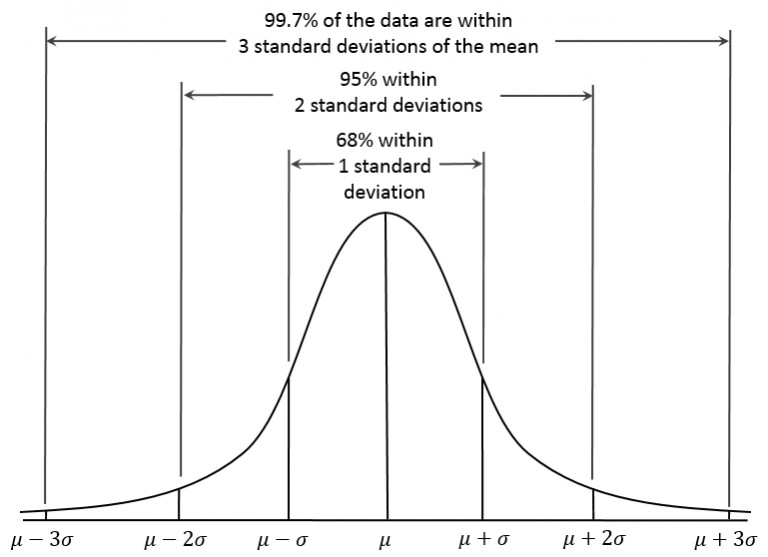

How to use the Normal Distribution
We use the normal distribution to relate the population mean μ, population standard deviation σ, and probability density of a data set. The image above uses the empirical rule to provide the actual percentage of data that falls within each respective number of standard deviations.
As we can see, more than half of the data falls within 1 standard deviation from the mean, and nearly all of the data falls within 3 standard deviations from the mean. In summary, data that follows the normal distribution is symmetric about the mean and falls within roughly 3 standard deviations.
Examples of Normal Distributions
Here are five examples of natural phenomena that follow the normal distribution:
- The height of male or female humans.
- The diameter of Douglas fir trees.
- The lifespan of car tires.
- The grades on a class' final exam.
- The time it takes someone to read this sentence.

