What is the Area Between Two Curves?

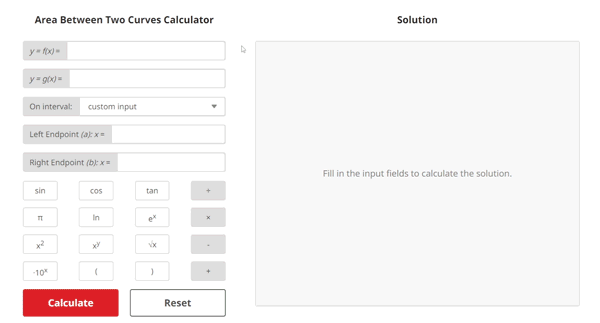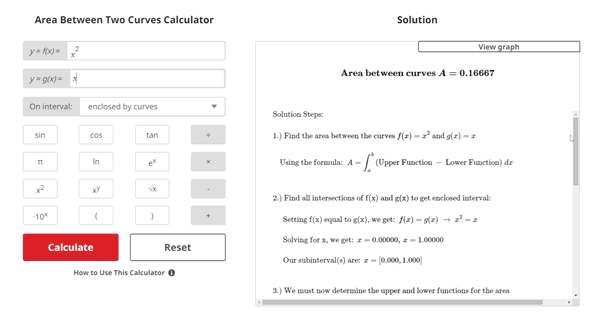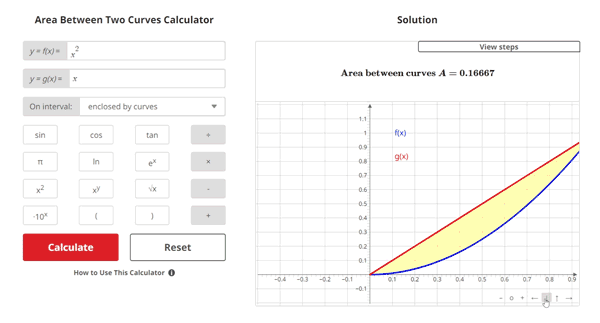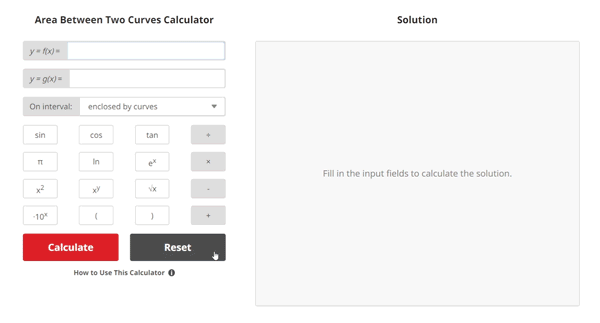
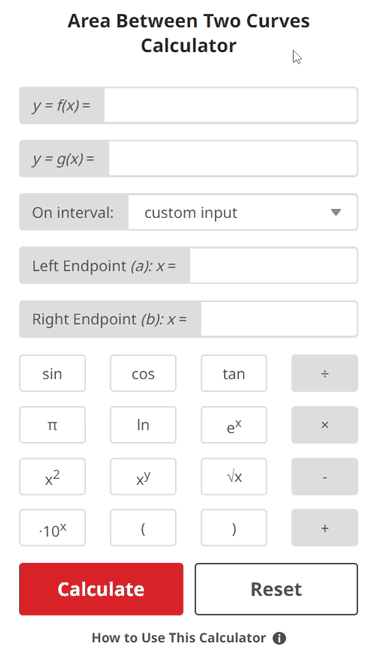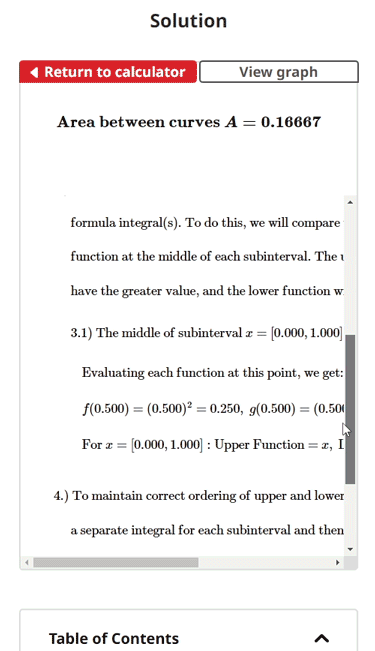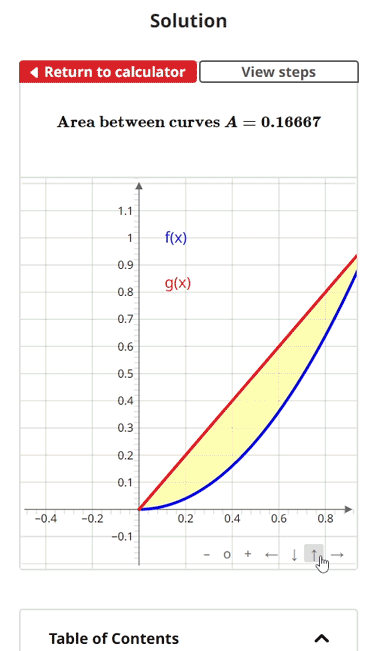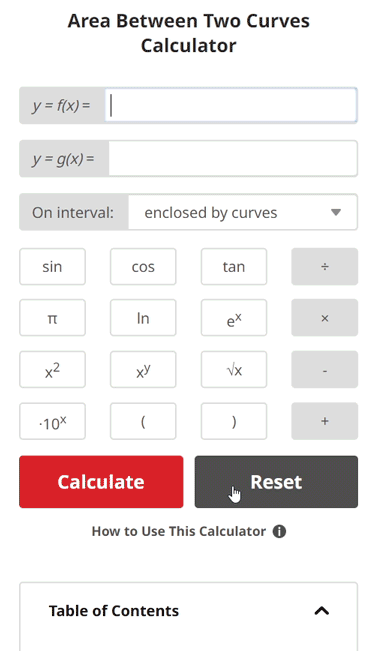
The yellow shaded region in the image below is an example of the area between two curves. This area is a 2-dimensional space bound by the curve of the upper function, the curve of the lower function, a left interval endpoint, and a right interval endpoint.

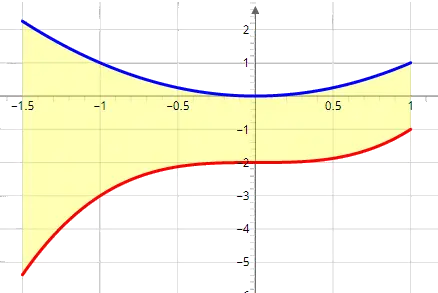
Why do we Learn About the Area Between Two Curves?

When we first learn about integrals to find the area under a curve, we get our initial insight into the usefulness of calculus for working with complex, real world systems. A basic example of this is using a Riemann Sum to approximate the distance a vehicle traveled by finding the area under its speed versus time curve.

But what could we possibly do by finding the area between two curves? Well, let's say that we drag race cars at a track on the weekends. Prior to each race, we ensure our data acquisition system inside the vehicle is set to record our speed at set time intervals over the entire duration of each run against our opponent we are racing against. Our opponent also has the same data acquisition system that is recording the same data at the same intervals of time.

After each quarter mile race, we would like to know the distance of the gap between our car and our opponent. To do this, we gather the data (speed versus time) from both cars and find the area between the two speed curves over the entire duration of the quarter mile run in question. This will show us the mutual displacement of our cars when the winner reached the finish line.

In other words, by finding the area between these two speed curves, we can determine the distance of the gap between the two vehicles during a specified time interval in the race.

How to Calculate the Area Between Two Curves

The formula for calculating the area between two curves is given as:

$$\begin{align} & A = \int_{a}^{b} \left( \text{Upper Function } - \text{ Lower Function} \right) \; dx, \hspace{3ex} a \leq x \leq b \end{align}$$

Where A is the area between the curves, a is the left endpoint of the interval, b is the right endpoint of the interval, Upper Function is a function of x that has the greater value on the interval, and Lower Function is a function of x that has the lesser value on the interval.

We may specify an interval x = [a, b] (which is the equivalent of a ≤ x ≤ b) when solving for area between two curves. However, if the two curves have at least two intersection points, we may also use the interval defining the area enclosed by the two curves.

Let's look at the image below as an example. The blue curve represents f(x) = x and the red curve represents g(x) = x³. These two functions' curves intersect at three points: x = -1, x = 0, and x = 1. Therefore, the area enclosed by them is defined by the interval x = [-1, 1].

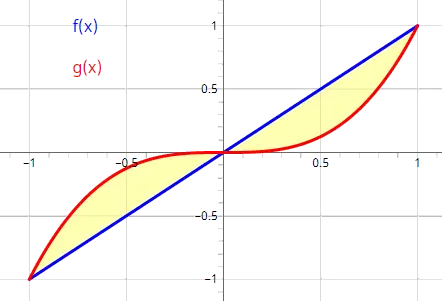
Once we know the interval we are solving on, we must determine the upper and lower functions for the subinterval(s). In some cases, there will only be a single subinterval which is the main interval itself. In other cases, there will be more than one subinterval where the curves cross each other and change positions as upper and lower functions, such as in the image directly above.

We may visually determine the upper and lower functions for each subinterval by viewing a graph of the curves. If a graph of the curves is not available, we may evaluate the value of each function in the middle of each subinterval. For example, a subinterval of x = [2, 4] has a middle point of x = 3. Therefore, we would plug x = 3 into each function and evaluate which has a greater value and which has a lesser value at that point.

Once we know the upper and lower functions for the single or multiple subinterval(s), we may set up an area formula for each subinterval. After solving each area formula integral, we sum the results from each to determine the total area between the curves on our interval. For a problem with n number of subintervals, this sum will look like:

A_total = A₁ + A₂ + ... + A_n

For the functions f(x) = x and g(x) = x³ on the interval defined by their enclosed area, this would be:

$$\begin{align} & A_{1} = \int_{-1}^{0} \left( \text{Upper Function } - \text{ Lower Function} \right) \; dx = \int_{-1}^{0} \left( x^{3} \; - \; x \right) \; dx \end{align}$$

$$\begin{align} & A_{2} = \int_{0}^{1} \left( \text{Upper Function } - \text{ Lower Function} \right) \; dx = \int_{0}^{1} \left( x \; - \; x^{3} \right) \; dx \end{align}$$

A_total = A₁ + A₂

Example Problem

$$\begin{align} & \text{Solution Steps:} \hspace{67ex}\\ \\ & \text{1.) Find the area between the curves } f(x) = x^2\text{ and } g(x) = x\\ \\ & \hspace{2ex} \text{Using the formula: } \; A = \int_{a}^{b} \left( \text{Upper Function } - \text{ Lower Function} \right) \; dx \hspace{5ex}\\ \\ \\ & \text{2.) Find all intersections of f(x) and g(x) to get enclosed interval:}\\ \\ & \hspace{3ex} \text{Setting f(x) equal to g(x), we get: } \: f(x) = g(x) \; \rightarrow \;x^2 = x\\ \\ & \hspace{3ex} \text{Solving for x, we get: } \: x = 0.00000, \: x = 1.00000\\ \\ & \hspace{3ex} \text{Our subinterval(s) are: } \:x = [0.000, 1.000]\\ \\ \\ & \text{3.) We must now determine the upper and lower functions for the area} \\ \\ & \hspace{3ex} \text{formula integral(s). To do this, we will compare the value of each} \\ \\ & \hspace{3ex} \text{function at the middle of each subinterval. The upper function will} \\ \\ & \hspace{3ex} \text{have the greater value, and the lower function will have the lesser value.}\\ \\ & \hspace{3ex} \text{3.1) The middle of subinterval } x = [0.000, 1.000] \text{ is located at } x = \frac{0.000 + 1.000}{2} = 0.500\\ \\ & \hspace{5ex} \text{Evaluating each function at this point, we get:} \\ \\ & \hspace{5ex}f(0.500) = (0.500)^2 = 0.250, \; g(0.500) = (0.500) = 0.500\\ \\ & \hspace{5ex} \text{For } x = [0.000, 1.000]:\text{Upper Function = } x, \;\text{Lower Function = } x^2\\ \\ \\ & \text{4.) To maintain correct ordering of upper and lower function, we will perform} \\ \\ & \hspace{3ex} \text{a separate integral for each subinterval and then sum those integrals.}\\ \\ & \hspace{3ex} A_{1} = \int_{0.00000}^{1.00000} \left(\left(x\right) - \left(x^2\right)\right) \; dx \; \rightarrow \; \left. {\left( {\left(- \frac{1}{3}\right) \cdot {x}^{3} + \left(\frac{1}{2}\right) \cdot {x}^{2}} \right)} \right|_{0.00000}^{1.00000} = 0.16667\\ \\ \\ & \text{5.) Summing the definite integral results, we get:} \\ \\ & \hspace{3ex} A = \fbox{0.16667}\\ & \end{align}$$

How the Calculator Works

The Area Between Two Curves Calculator is primarily built with the web programming languages HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). The HTML builds the architecture, the CSS creates all visual styling properties of the calculator, and the JS provides calculation functionality.

When the "calculate" button is clicked, a JS function is activated. The user inputted values are read and used for the same exact process outlined in the above example problems. Various intermediate values are saved and formatted for the solution steps.

The indefinite integrals are performed by a JS-native CAS (computer algebra system). The CAS applies integral rules by treating every character like a symbol, providing nearly perfect accuracy. This process is known as symbolic computation.

The final answer is rounded and formatted, then all solution steps are formatted. The answer and steps are printed to the solution area and rendered by a LaTeX (a math visual rendering language/technology) rendering engine.