Algebra
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Vertex Form
Lesson Contents
What is Vertex Form?
The vertex form of a parabola is given as:
Vertex Form Definition
Vertex form is a way of writing the equation for a parabola. Compared to standard form, vertex form makes it easier to graph parabolas by hand. Here is what the different components tell us:
a – Scaling factor (the larger a is, the skinnier the parabola becomes), a also determines concavity of parabola (parabola opens upward for positive a, parabola opens downward for negative a).
x – Independent variable.
h – X coordinate for vertex of parabola, also the x coordinate of the vertical axis of symmetry.
k – Y coordinate for vertex of parabola.
Graphing a Quadratic Function in Vertex Form
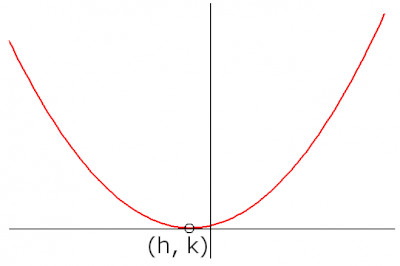
When graphing a quadratic function with vertex form, the vertex’s x and y values are h and k respectively. In other words, for the vertex, (x, y) = (h, k). See the image above for a parabola graphed with the vertex labeled.
To graph a parabola using vertex form, we first graph the vertex point. Then, we can plug several x values on either side of the vertex into the function to find their respective y values. This gives us additional points to use for graphing the curvature of the parabola. Draw a smooth curve through these points to finish graphing it.
How to Find Vertex Form
| Standard Form | Vertex Form |
|---|---|
|
|
The table above is a side by side comparison of standard form and vertex form.
Standard form is formatted to flow from highest order term to lowest order term.
The first term is the second power term, the second term is the first power term, and the third term is the zeroth power term (since x to the zeroth power is simply one, leaving the coefficient c as the third term).
Vertex form is formatted for convenience of graphing quadratic functions and their resulting parabola.
Converting Standard Form to Vertex Form
There is no formula for converting standard form to vertex form. We must follow the rules of algebra and rearrange a standard form equation to make it match the definition of vertex form.
The required number of algebraic maneuvers depends on the parabola itself and how easy it is to factor the x – h. In the example problem below, we show how to convert standard form to vertex form.
Example Problem
What is y = 9x2 + 9x – 1 rewritten in vertex form?
Solution:
1. First, factor out the 9 from both x terms. y = 9(x2 + x) – 1
2. We will convert to vertex form by completing the square. The coefficient in front of the first power term (x) is our value for b. In this case, b = 1.
3. Add (b/2)2 to the quantity inside of the parenthesis. As per the rules of algebra, we must also add the same number to the other side of the equation. Since (b/2)2 = (1/2)2 = 1/4, and 9(1/4) = 9/4, we will add 9/4 to the left side of the equation.
4. We now have y + 9/4 = 9(x2 + x + 1/4) – 1.
5. Factor the parenthesis into a square. 9(x2 + x + 1/4) = 9(x + 1/2)2
6. Isolate y and simplify the equation. y = 9(x + 1/2)2 – 13/4
7. The equation in vertex form is y = 9(x + 1/2)2 – 13/4.