Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Cross Product Calculator
i +
j +
k
i +
j +
k
Solution:
a × b = [a2b3 – a3b2]i – ...
Cross Product Lesson
Lesson Contents
What is the Cross Product?
The cross product of two vectors is a vector that is orthogonal (perpendicular) to both original vectors.
This means that a 90° angle can be drawn between the resultant vector and each of the original vectors. The magnitude of the resultant vector is equal to the area of the parallelogram that is projected from the two original vectors.
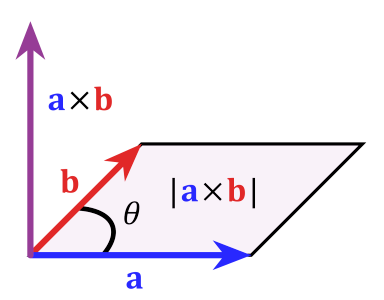
The image below is a visualization of what a cross product resultant vector represents. When looking at the image, we might observe that the cross product is normal to the plane on which both original vectors lie on.
The parallelogram lies flat on that plane, and the cross product vector’s magnitude/length is equal to the area of the parallelogram.
A cross product tells us the normal direction
and area of two vectors’ projected parallelogram.
Why do we Learn About the Cross Product?
Since the cross product is needed for countless real-world physics and engineering applications, let’s take a look at just one of these applications: controlling a space telescope’s orientation to point it at a celestial object of interest.
Instead of using thrusters that expel propellant, the Hubble Space Telescope uses special devices called reaction wheels for controlling its orientation with extreme precision and reliability.
The Hubble Space Telescope’s Reaction Wheels And Sensors
Credit: NASA
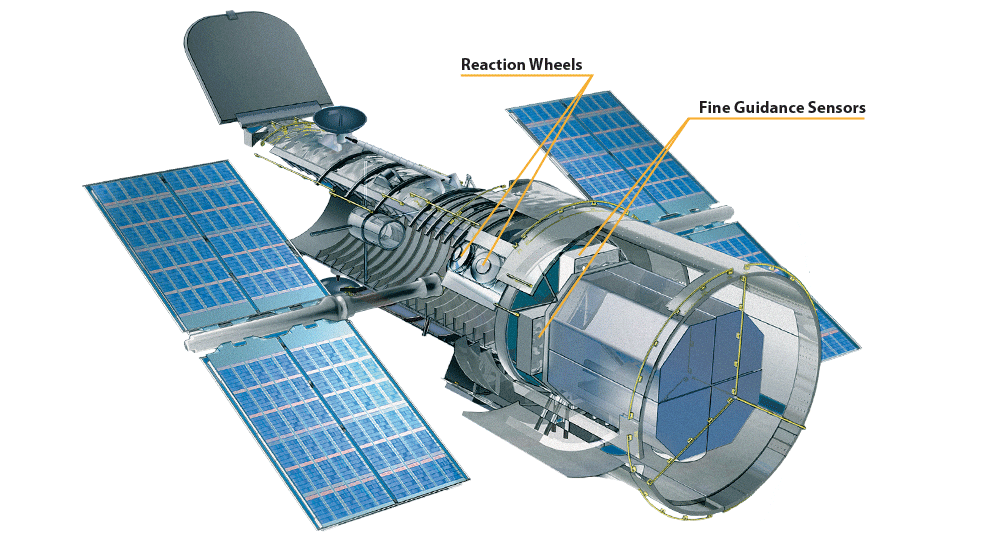
Credit: NASA
A reaction wheel is a motorized wheel with substantial mass near its outer edges, allowing it to store large amounts of angular momentum while spinning. If a reaction wheel mounted on a space telescope is spun up by its motor in a certain direction of rotation, the telescope will spin in the opposite direction of rotation as a result.
This is due to the law of conservation of momentum. The change in angular momentum of the telescope is equal in magnitude and opposite in direction to the change in angular momentum of the reaction wheel.
Now, why would we need the cross product for all of this? Well, the formula for angular momentum is given as:
L = r×p
Where L is the angular momentum vector, r is the position vector, p is the linear momentum vector, and the × between the position and momentum vectors denotes the cross product.
Once we have characterized the telescope’s position vector and linear momentum vector, we may use the cross product to solve for the angular momentum of the telescope under various rotational motion conditions.
Finally, we can design the reaction wheel for optimal orientation authority, precision, and reliability by tweaking the reaction wheel’s theoretical position vector and linear momentum vector, solving for their cross product, and observing the output angular momentum in the context of the telescope’s angular momentum.
How to Calculate the Cross Product
For a vector a = a1i + a2j + a3k and a vector b = b1i + b2j + b3k, the formula for calculating the cross product is given as:
a×b = (a2b3 – a3b2)i – (a1b3 – a3b1)j + (a1b2 – a2b1)k
To calculate the cross product, we plug each original vector’s respective components into the cross product formula and then simplify the right side of the equation. The result will be a vector a×b = c1i + c2j + c3k.
A set of two vectors must occupy three-dimensional space to have a cross product. However, a vector with one or two components of zero (such as a = 3i + 0j + 0k) is still considered to occupy three-dimensional space.
This is because the nonzero components project them along a certain axis (one-dimensional) or plane (two-dimensional). For example, the vector a = 3i only has a component (3i) on the x-axis.
But, we may add a 0j and 0k term to it, resulting in the equivalent vector a = 3i + 0j + 0k, and can now use it as an original vector for a cross product.
Example Problem
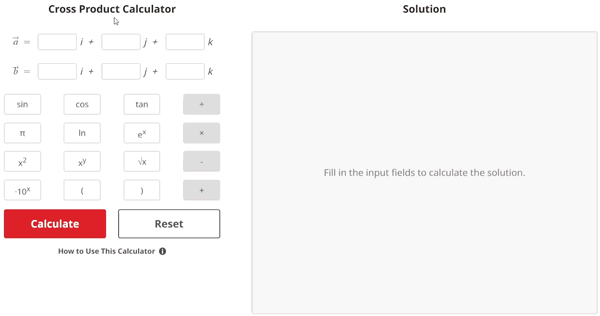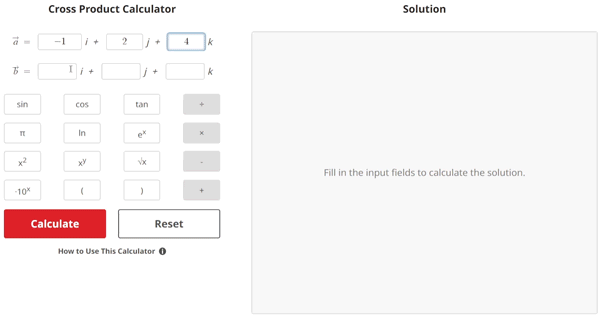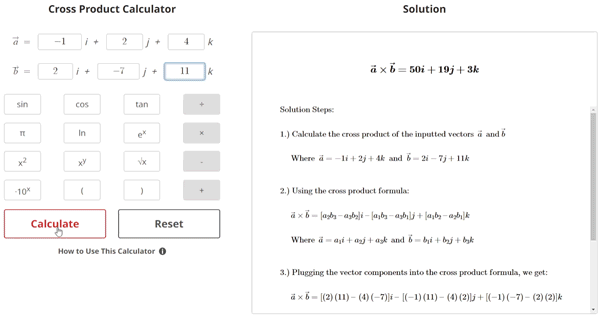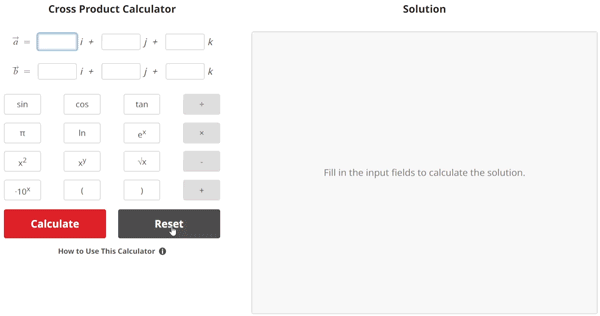
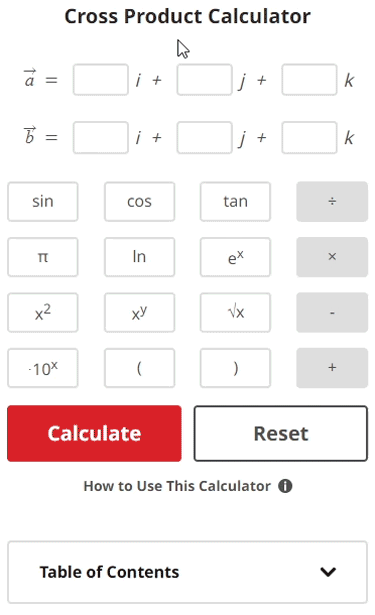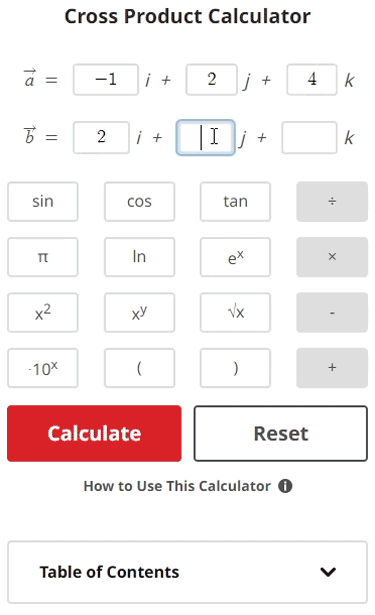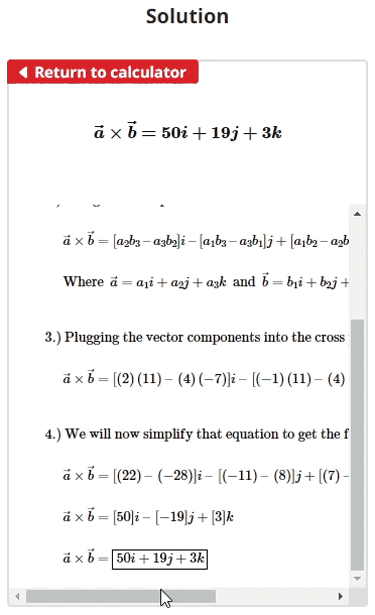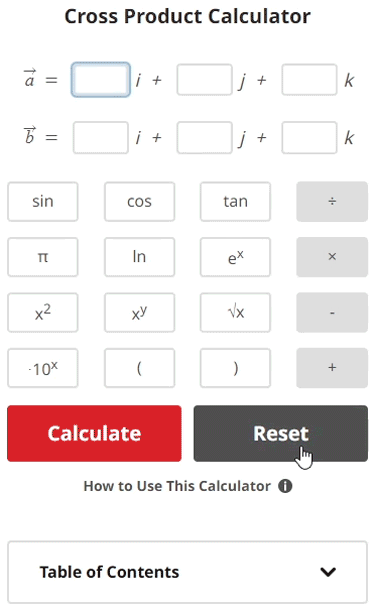
$$\begin{align}& \text{1.) Calculate the cross product of the two vectors } \: \vec{a} \: \text{ and } \vec{b} \\ \\ & \hspace{3ex} \text{Where } \; \vec{a} = -1i +2j +4k \; \text{ and } \; \vec{b} = 2i -7j +11k\\ \\ \\ & \text{2.) Using the cross product formula:} \\ \\ & \hspace{3ex} \vec{a} \times \vec{b} = [a_{2}b_{3} \: – \: a_{3}b_{2}]i \: – \: [a_{1}b_{3} \: – \: a_{3}b_{1}]j + [a_{1}b_{2} \: – \: a_{2}b_{1}]k \\ \\ & \hspace{3ex} \text{Where } \: \vec{a} = a_{1}i + a_{2}j + a_{3}k \: \text{ and } \: \vec{b} = b_{1}i + b_{2}j + b_{3}k\\ \\ \\ & \text{3.) Plugging the vector components into the cross product formula, we get:} \\ \\ & \hspace{3ex} \vec{a} \times \vec{b} = \left[ \left( 2\right) \left( 11\right) \: – \: \left( 4\right) \left( -7\right) \right] i \: – \: \left[ \left( -1\right) \left( 11\right) \: – \: \left( 4\right) \left( 2\right) \right] j + \left[ \left( -1\right) \left( -7\right) \: – \: \left( 2\right) \left( 2\right) \right] k\\ \\ \\ & \text{4.) We will now simplify that equation to get the final vector:} \\ \\ & \hspace{3ex} \vec{a} \times \vec{b} = \left[ \left( 22\right) \: – \: \left( – 28\right) \right] i \: – \: \left[ \left( – 11\right) \: – \: \left( 8\right) \right] j + \left[ \left( 7\right) \: – \: \left( 4\right) \right] k\\ \\ & \hspace{3ex} \vec{a} \times \vec{b} = \left[ 50\right] i \: – \: \left[ – 19\right] j + \left[3\right] k \hspace{1ex} \\ \\ & \hspace{3ex} \vec{a} \times \vec{b} = 50i + 19j + 3k\end{align}$$
How the Calculator Works
The Voovers cross product calculator is written in the web programming languages HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). The HTML builds the calculator’s physical architecture, the CSS styles that architecture, and the JS adds all functionality to the calculator.
Your device’s internet browser has a built-in JS engine that runs the code immediately when you click the calculate button. This allows for instant solutions and no waiting on the page to refresh.
The calculator’s routine builds your inputted vector components into an array, essentially turning the inputs into JS vectors of sorts. The array is then fed to the cross product formula. The right side of the resulting equation is simplified to get the output cross product vector.
Along the way, snapshots of the problem are saved as JS variables to be used in the solution steps. The solution and solution steps are formatted into LaTeX (a math equation rendering technology) code and displayed in the solution box.