Definition of Cotangent

In trigonometry, the cotangent is the reciprocal of the tangent. Cotangent is abbreviated as cot. The relation of cotangent and tangent is as follows:

cot(θ) = ¹⁄_tan(θ) and cot(θ) = ^cos(θ)⁄_sin(θ) and tan(θ) = ¹⁄_cot(θ)

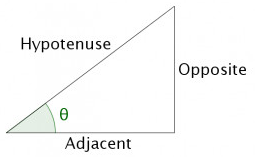
In a right triangle, the cotangent of an internal angle is the adjacent side divided by the opposite side, such that cot(θ) = ^adjacent⁄_opposite.

Cotangent's Inverse — cot^-1

The inverse function of the cotangent is called arc cotangent. In abbreviated form, this relation is given as:

arccot = cot^-1

The arc cotangent follows the same relation as all other inverse trigonometric functions. It is the length that produces an angle where the cot of that angle is the length. Here is what the relation looks like when used:

1. cot(65°) = 0.466
2. arccot(0.466) = 65°

Graph of the Cotangent Function

The image below is what y = cot(x) looks like when graphed for several periods.

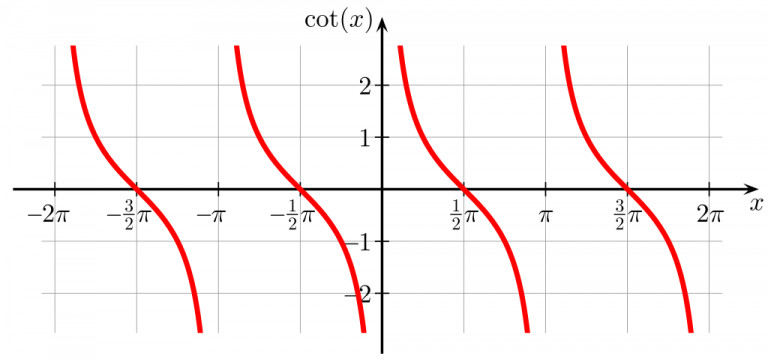
Notice how the curves are asymptotic to x = -π, x = 0, x = π, and so forth? This is because at every whole multiple of pi, the value of the function looks like:

y = cot(π) = ^cos(π)⁄_sin(π) = ^-1⁄₀

Since dividing by zero is undefined, the function does not exist on those x values. The curve will go infinitely up or down in the vertical direction, but never touch the x values that it is asymptotic to.