Series vs. Parallel: What's the Difference?

In circuits, the two basic ways to connect components are in series and in parallel. The words "series" and "parallel" simply tell us how many paths there are for the electric current to take. In a series circuit, the electric current has only one path to take. In a parallel circuit, there is more than one path for the electric current to take.

Series Circuit Basics

When components are connected in series, the electric current must take a single path. The series circuit below consists of a DC voltage source with three resistors connected in series.

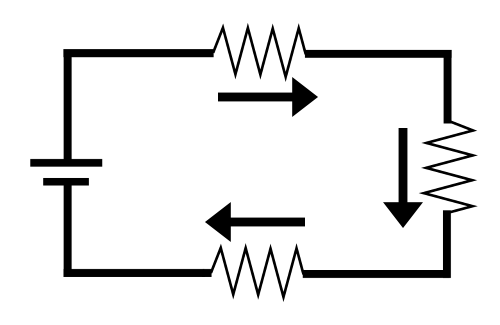
The electric current has only a single path through the resistors — therefore it is a series circuit. An easy way to remember how a series circuit works: the components are in a series, connected one after the other just like the games in a baseball series.

Parallel Circuit Basics

When components are connected in parallel, the electric current takes more than one path. The parallel circuit below consists of a DC voltage source with three resistors connected in parallel, with three parallel branches (one per resistor).

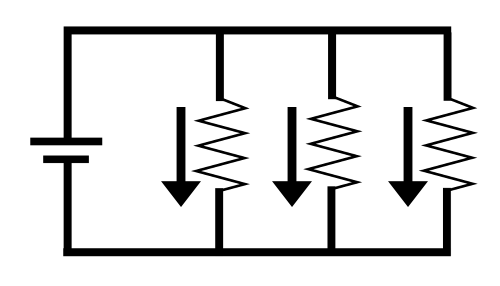
The electric current takes each of the three paths created by each resistor's branch in the circuit. It is called a parallel circuit because it is graphically represented to have multiple paths of electric current that are parallel to each other.

Calculating Voltage, Current, and Resistance

There are three basic parameters we study when dealing with series and parallel circuits.

1. The voltage across a component
2. The current through a component
3. The resistance of a component

The relationship between these three parameters is governed by Ohm's law, given as V = IR, where V is voltage, I is current, and R is resistance. However, parallel circuits add some complexity to calculating these. Let's go through how to deal with calculating the three parameters for series circuits and for parallel circuits.

How to Solve a Series Circuit

For a series circuit like the one below, we follow these three basic rules.

1. The total resistance of the circuit equals the sum of all resistors.
   R_total = R₁ + R₂ + ... + R_n
2. The current through the circuit is equal to the DC voltage divided by the total resistance of the circuit.
   I_total = ^V_total⁄_Rtotal
3. The voltage across a component is V = IR, where R is the resistance of the component.
   V_n = I_total×R_n

Let's work together to find the voltage across each resistor and the current through the circuit, based on the resistance of each component.

We can call the three resistors R₁, R₂, and R₃ respectively. Also, we will call the DC voltage source V₀. To find the current through the circuit, we must first find the total resistance.

Following series circuit rule #1, we know that adding all three resistors will give us the total resistance. So, R_total = R₁ + R₂ + R₃.

Then, following rule #2, we get I_total = ^V₀⁄_Rtotal. We now know the total resistance and current of the circuit!

Lastly, we will quickly find the voltage across each resistor. Rule #3 and Ohm's law tell us that V = IR. So, V₁ = I_total×R₁, V₂ = I_total×R₂, and V₃ = I_total×R₃.

How to Solve a Parallel Circuit

For a parallel circuit like the one below, we follow these four basic rules.

1. The reciprocal of the total resistance of the circuit equals the sum of the reciprocals of every branch's resistance.
   ¹⁄_Rtotal = ¹⁄_Rb1 + ¹⁄_Rb2 + ... + ¹⁄_Rbn
2. The current through the circuit is equal to the DC voltage source divided by the total resistance of the circuit, but the current through each branch is a fraction of the total current and dependent on that branch's resistance (see rule #4).
   I_total = ^V_total⁄_Rtotal
3. The voltage across each branch is equal to the DC voltage source for the branches.
   V_bn = V_total
4. The current through each branch is equal to the voltage divided by the branch's resistance.
   I_bn = ^V_bn⁄_Rbn

Let's work together to find the current through each branch.

We can call the three branches and their resistors B1, B2, B3, R₁, R₂, and R₃ respectively. Also, we will call the DC voltage source V₀.

Following parallel circuit rule #4, we know that we can apply Ohm's law to each individual branch because rule #3 tells us the voltage across each branch. Applying rule #3 gives us V_b1 = V₀, V_b2 = V₀, and V_b3 = V₀.

Now, applying rule #4, we get I_b1 = ^V_b1⁄_R1, I_b2 = ^V_b2⁄_R2, and I_b3 = ^V_b3⁄_R3. We now know the current through each parallel branch of the circuit!