Parallelepiped Volume Formula

There are two formulas for finding volume of a parallelepiped. They are given as:

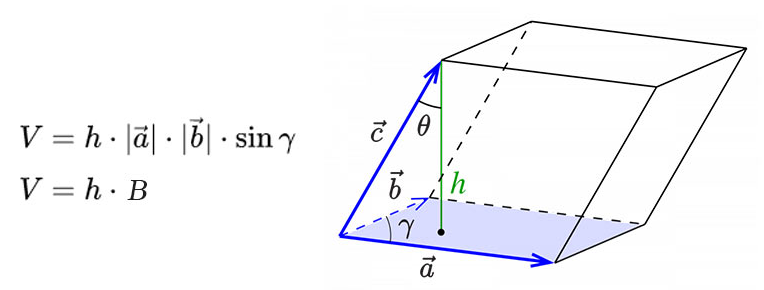
V = h·|a|·|b|·sin(γ)

V = h·B

Where V is the volume, h is the height, a and b are the base edge vectors, γ is the angle between vectors a and b, and B is the area of the base.

What is a Parallelepiped?

A parallelepiped is a three-dimensional shape made of 6 faces. It is the result of tilting the edges of a rectangular prism. Imagine pushing against the top corner of a box that is not perfectly rigid. The box will slant in the direction that it is pushed. This forms a parallelepiped.

As we can see in the image above, there are three pairs of congruent parallelograms on opposing sides of the figure. This is the most common style of parallelepiped. However, not all parallelepiped shapes have three pairs of opposing congruent sides.

It is easier to calculate the volume of parallelepiped type shapes if we understand that a parallelepiped is formed by six parallelograms. If we understand how to calculate volume of a rectangular prism and can visualize what a parallelepiped is, we need not memorize the formula. Finding the area of the base parallelogram and multiplying by the shape's height will give us the volume.

Volume of a Parallelepiped Example Problem

A given parallelepiped is made up of 3 pairs of congruent parallelograms. The base parallelogram has an area of 8. The height of the parallelepiped is 4. What is its volume?

Solution:

1. Since we are given base area and height, we can use the simplified formula V = h∙B.
2. Let's plug the base area and height into the formula.
3. V = (4)(8) = 32.
4. The volume of the parallelepiped is 32.