Hexagonal Prism Volume Formula

The formula for volume of a hexagonal prism is given as:

$$\begin{align} & V = \frac{3\sqrt{3}}{2}a^{2}h \end{align}$$

Where V is the volume, a is the hexagon base's edge length, and h is the height of the prism.

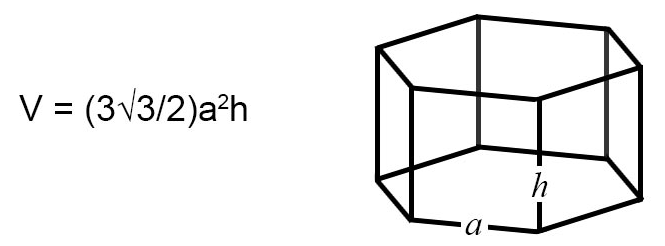
What is a Hexagonal Prism?

A hexagonal prism is the three-dimensional shape that is created from extending the face of a hexagon upwards into the third dimension. Since a hexagon is two dimensional, it becomes a prism once it extends upwards into the third dimension.

The difference between a hexagonal prism and a rectangular prism is the shape of the cross section. The cross section of a prism is what we see if we cut the prism on a plane that is parallel to its base plane. It will appear as the shape that the base of the prism is made of, which is a hexagon in the case of a hexagonal prism, and a rectangle in the case of a rectangular prism.

Volume of a Hexagonal Prism Example Problem

Let's go through an example problem together to practice finding the volume of a hexagonal prism.

Find the volume of a hexagonal prism with a base edge length of 20 and a prism height of 10.

Solution:

1. We have all values needed to use the volume formula directly. Let's plug the given dimensions into the volume formula.
2. V = ^3√3⁄₂a²h
3. V = ^3√3⁄₂(20²)(10) = 10,392.3
4. The volume of the hexagonal prism is 10,392.3.