Definition of Vertical Angles

Vertical angles are the opposing angles where two lines cross. Vertical angles are always equal in value.

The Vertical Angles Theorem

The vertical angles theorem tells us that angles opposite each other where two lines cross are congruent (equal in value).

In the image below, α and β are vertical and equal angles.

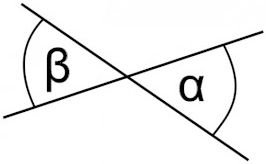
The “vertical” in vertical angles should not be confused with lines or angles being oriented up and down, as the word vertical implies. In this context, vertical means that the two angles are opposite each other about a shared apex.

Another name for vertical angles is vertically opposite angles. This name is very intuitive because it describes that the angles are opposite each other where two lines cross.

How to use the Theorem

There are four angles where two lines cross (making two pairs of vertical angles). These four angles are labeled as A, B, C, and D in the image below. Congruent angles are marked with a like number of dashes as shown in the image below.

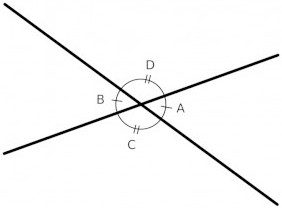
These four angles are what make the two pairs of vertical angles. A = B and C = D. Because of what the vertical angles theorem tells us, we only need to know the value of one of these angles to determine all the others. The sum of angles around the crossing of two lines is always 360°.

The rules of geometry tell us that A + B + C + D = 360°. With simple arithmetic, we can find the other three angles from only knowing one angle. This is what makes the vertical angles theorem so powerful.

When to use the Theorem

If we are solving a geometry problem that has intersecting lines and we are given one of the angles, we can find the other three angles by using the vertical angles theorem. This is extremely useful for intersecting shapes and other angle-based problems. It works for triangles, rectangles, etc. It is the basis of the relationship between internal and external angles of shapes.

Vertical Angles Example Problems

Let's go through a couple of example problems together to reinforce our understanding of vertical angles.

Example Problem 1

Two lines cross and form the angles A, B, C, and D. A opposes B, and C opposes D. If angle B is 50°, what are the values of angles A, C, and D in degrees?

Solution:

1. A and B are vertical angles, so A = B. B = 50°, therefore A = 50°.
2. C and D are vertical angles, so C = D. The sum of A, B, C, and D must be 360°.
3. 360° = A + B + C + D
4. 360° = 50° + 50° + C + D
5. 260° = C + D
6. ^260°⁄₂ = 130°, C = 130° and D = 130°
7. A = 50°, C = 130°, and D = 130°.

Example Problem 2

Two lines intersect. One of the angles at the intersection is measured to be 60°. Is this the smallest angle at the intersection?

Solution:

1. The vertical angles theorem tells us that the angle opposite of the 60° angle must also be 60°. The sum of this pair of vertical angles is 120°.
2. 360 - 120 = 240
3. ²⁴⁰⁄₂ = 120
4. Therefore, the intersection is made up of angles 60°, 60°, 120°, and 120°.
5. The 60° measured angle is tied with its opposing angle for being the smallest angle at the line intersection.