What is a Triangular Prism?

A triangular prism is formed by extending the face of a triangle in either direction normal to its face. We can imagine it as stacking a very large number of very thin triangles face to face.

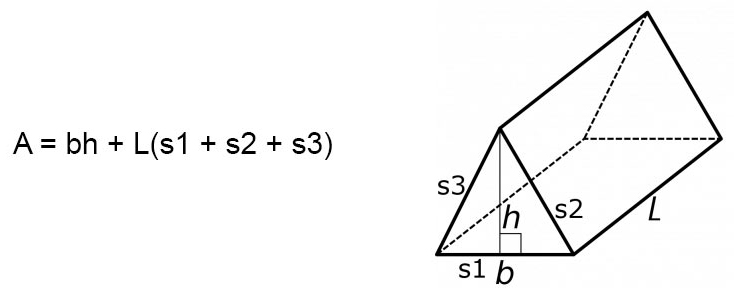
A triangular prism has five faces. These five faces are made up of two triangles and three rectangles. In the triangular prism shown below (Figure 1), the front triangle face with sides s1, s2, and s3 is connected to the rear triangle face by the three rectangle faces. A triangle face is considered the base, and a rectangle face is considered a lateral face.

Triangular Prism Surface Area Formula

The formula for finding the surface area of a triangular prism is given as:

A = bh + L(s1 + s2 + s3)

Where A is the surface area, b is the bottom edge of the base triangle, h is the height of the base triangle, L is the length of the prism, and s1, s2, and s3 are the three edges of the base triangle.

How the Triangular Prism Surface Area Formula is Derived

The triangular prism shown in the image above (Figure 1) has opposing triangle faces that are equilateral, so all triangle sides are equal. However, the given formula allows us to calculate the surface area of a triangular prism with any style of triangular face.

The triangle sides are broken into s1, s2, and s3, which will all be equal in the case of an equilateral triangle. Since a triangular prism can be broken down into two triangular faces and three rectangular faces, our formula combines the surface area of both triangular faces into the single term bh.

The surface area of the three rectangular faces is combined into the term that multiplies L by the sum of the three sides of the triangle (s1, s2, and s3). Adding this term to the triangle face areas gives us the sum of surface areas of all faces on the triangular prism.

Triangular Prism Surface Area Example Problem 1

The bases of a triangular prism are formed by a right triangle with leg lengths of 4 and 7. The lateral faces of the prism are formed by a rectangle with a length of 5. Find the surface area of the triangular prism.

Solution:

1. Since the base of the prism is formed by a right triangle and we know the leg lengths of the triangle, we can use the legs as the base and height. Therefore, b = 4 and h = 7. These will also be our first two sides, so s1 = 4 and s2 = 7.
2. We are still missing s3, which is the hypotenuse of the right triangle. Using the Pythagorean theorem, we get:
   (s3)² = 4² + 7²
   s3 = 8.062.
3. Now let's plug our known values into the surface area formula.
   A = (4)(7) + (5)(4 + 7 + 8.062).
   A = 123.31
4. The surface area of the right-angled triangular prism is 123.31.

Triangular Prism Surface Area Example Problem 2

If we are given a triangular prism that has a base formed by an equilateral triangle, how can we simplify the surface area formula before solving it?

Solution:

1. Since an equilateral triangle is made of three equivalent side lengths, we know that our s1 = s2 = s3. Therefore, s1 + s2 + s3 = 3s1. Also, we can set b = s1. So, 3s1 = 3b.
2. We can use this to replace (s1 + s2 + s3) in the formula with 3b. This gives us our simplified formula as A = bh + 3bL.