Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Surface Area of a Pyramid
Pyramid Surface Area Formula
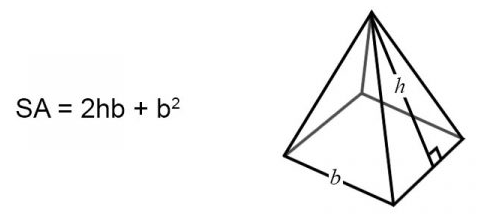
A right square pyramid has a square-shaped base and 4 congruent triangle faces. The formula for surface area of a right square pyramid is given as:
SA = 2hb + b2
Where SA is the surface area, h is the height of the triangular face, and b is the edge length of the square base.
Example Problems
Problem 1:
Find the surface area of a right square pyramid with an edge length of 10 and a triangle face height of 20.
Solution:
1.) Plugging what we know into the formula, we get:
SA = 2hb + b2
SA = 2(20)(10) + 102 = 400 + 100 = 500
2.) The surface area is 500.
Problem 2:
If the pyramid from problem 1 has its edge length reduced from 10 to 5, how does the surface area change?
Solution:
1.) Plugging the edge length of 5 and height of 20 into the formula, we get:
SA = 2hb + b2
SA = 2(20)(5) + 52 = 200 + 25 = 225
2.) Reducing the edge length from 10 to 5 reduced the surface area from 500 to 225.
