Cylinder Surface Area Formula

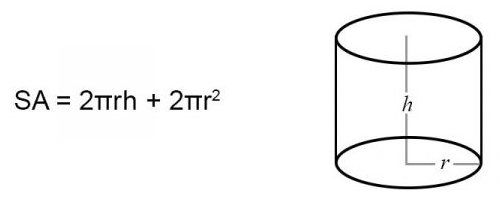
The formula for surface area of a cylinder is given as:

SA = 2πrh + 2πr²

Where SA is the surface area, r is the radius of the base circle, and h is the height of the cylinder.

Surface Area of a Cylinder Example Problems

Let's go through a couple of example problems together to practice finding the surface area of a cylinder.

Example Problem 1

What is the surface area of a cylinder with a diameter of 20 and a height of 20?

Solution:

1. Let's convert diameter to radius. D = 2r, 20 = 2r, so r = 10.
2. Now let's plug the radius and height into the surface area formula.
3. SA = 2πrh + 2πr²
4. SA = 2π(10)(20) + 2π(10²) = 2π(200) + 2π(100)
5. SA = 1,884.956
6. The surface area is 1,884.956.

Example Problem 2

A cylinder is measured to have a surface area of 24 square meters. It's height and radius are equal. What is the height of the cylinder?

Solution:

1. Let's set up relations between height and radius that we can substitute into the formula.
2. h = r
3. rh = h²
4. r² = h²
5. Now let's plug what we know into the surface area formula and solve for h.
6. SA = 2πrh + 2πr²
7. 24 = 2πh² + 2πh²
8. 24 = 4πh²
9. 1.910 = h²
10. h = 1.382
11. The height of the cylinder is 1.382 meters.