Cube Surface Area Formula

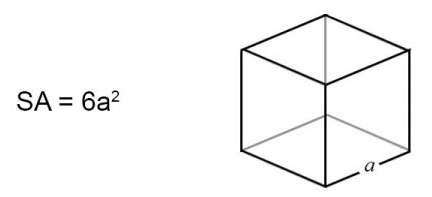
The formula for surface area of a cube is given as:

SA = 6a²

Where SA is the surface area, and a is the edge length.

A cube has 6 faces that are all squares. The surface area formula is 6 times the area of a square (area of a square = a²).

Surface Area of a Cube Example Problems

Let's go through a couple of example problems together to practice finding the surface area of a cube.

Example Problem 1

Find the surface area of a cube with an edge length of 8.

Solution:

1. Let's plug the edge length into the formula.
2. SA = 6a²
3. SA = 6(8²) = 384
4. The surface area of the cube is 384.

Example Problem 2

What is the edge length of a cube with a surface area of 864?

Solution:

1. Let's plug the surface area into the surface area formula and then solve for the edge length a.
2. SA = 6a²
3. 864 = 6a²
4. 144 = a²
5. a = √144
6. a = 12
7. The edge length is 12.