Surface Area of a Cone Lesson
Cone Surface Area Formula
The formula for surface area of a cone is given as:
$$SA=\pi r(r+\sqrt{h^{2}+r^{2}})$$
Where SA is the surface area, h is the height of the cone, and r is the radius of the circle at the cone's base.
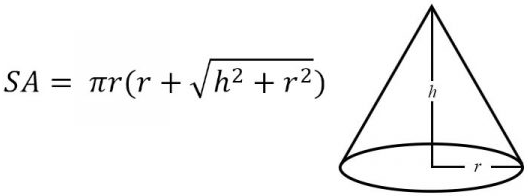
INTRODUCING

Surface Area of a Cone Example Problems
Let's go through a couple of example problems together to practice finding the surface area of a cone.
Example Problem 1
Find the surface area of a cone with a height of 6 and a radius of 4.
Solution:
- We have both required dimensions to use the surface area formula.
- Plugging the height and radius in, we get:
SA = πr[r + √(h2 + r2)]
SA = π(4)[4+ √(62 + 42)] = π(4)[11.2111] = 140.883 - The surface area of the cone is 140.883.
Example Problem 2
Find the surface area of a cone with a height of 1 and a radius of 1.
Solution:
- We have both required dimensions to use the surface area formula.
- Plugging the height and radius in, we get:
SA = πr[r + √(h2 + r2)]
SA = π(1)[1+ √(12 + 12)] = π(1)[2.414] = 7.584 - The surface area of the cone is 7.584.

